Forward Accumulation
First, make a computation graph.
Consider \(\ln (ab + \max (a,2))\)
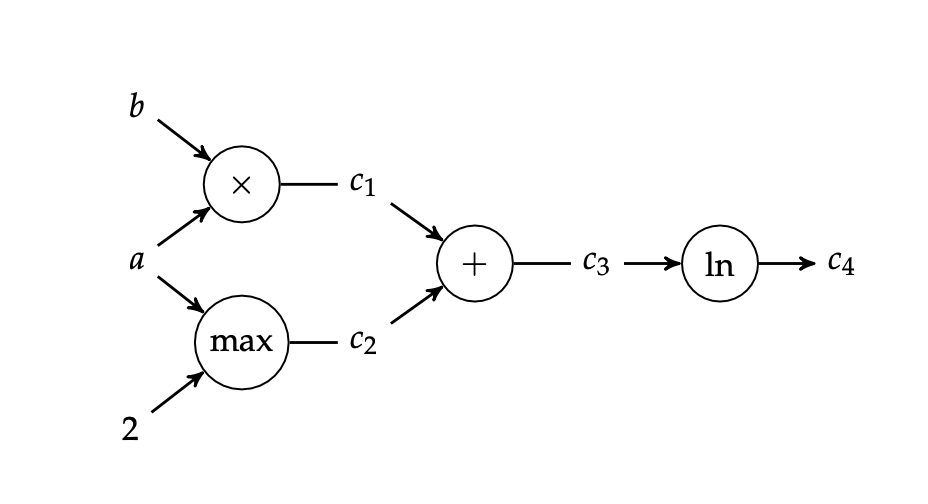
Say we want \(\pdv{f}{a}(3,2)\).
Let’s begin by tracking, left to right, both the value of each node and its derivative.
Layer 1:
- \(b = 2, \pdv{b}{a} = 0\)
- \(a = 3, \pdv{a}{a} = 1\)
Layer 2:
- \(c_1 = a\times b = 6, \pdv{c_1}{a} = b\pdv{a}{a} + a \pdv{a}{b} = 2\)
and so on; until we get to \(c_4\)
Dual Number Method
Dual Number
Consider:
\begin{equation} a+b \epsilon \end{equation}
Let’s declare:
\begin{equation} \epsilon^{2} = 0 \end{equation}
The standard field operations still apply:
\begin{equation} (a+b\epsilon) + (c+d\epsilon) = (a+c) + (b+d) \epsilon \end{equation}
The Method
We can write down a usual Taylor expansion:
\begin{equation} f(a+b\epsilon) = \sum_{k=0}^{\infty} \frac{f^{(k)}}{k!} (a+b \epsilon - a)^{k} \end{equation}
IMPORTANTLY:
\begin{equation} f(a+1\epsilon) = f(a) + f’(a) \epsilon \end{equation}
This means that we can use Dual Numbers to directly compute derivatives.