Suppose \(v_1, \dots v_{n} \in V\) is a basis of some vector space \(V\); \(w_1, \dots w_{n} \in W\) is just a good’ol list of length \(n= \dim V\) in \(W\).
There exists a unique linear map \(T \in \mathcal{L}(V,W)\) such that…
\begin{equation} Tv_{j} = w_{j} \end{equation}
for each \(j = 1, \dots n\)
Intuition
The layperson’s explanation of this result: 1) that, for everywhere you want to take the basis of one space, there’s always a unique linear map to take you there. 2) that, a linear map is determined uniquely by what it does to the basis of its domain.
Proof
We have two vector spaces, \(V\) and \(W\); \(v_1, \dots v_{n} \in V\) forms a basis of \(V\); \(w_1, \dots w_{n} \in W\) are just some vectors in \(W\).
Definition
We define some \(T: V \to W\) as follows:
\begin{equation} T(c_1v_1 + \dots + c_{n}v_{n}) = c_1 w_1 + \dots + c_{n} w_{n} \end{equation}
where, \(c_1, \dots c_{n} \in \mathbb{F}\). Note that the actual values of \(c\) doesn’t actually matter here.
Existence
We now show that the \(T\) defined above has the property of mapping \(Tv_{j} \to w_{j}\).
As the basis \(v_1, \dots v_{n}\) is a spanning list of \(V\), some \(T\) that takes an arbitrary linear combination of \(v\) as input does indeed have domain \(V\). Due to addition’s closure, a linear combination of \(w\) is \(\in W\). This makes \(T\) at least a function from \(V \to W\).
Of course, by taking all \(c_{i}\) to \(0\) except for the index \(c_{j}\) you are interested in to \(1\), you can show that this \(T\) takes \(v_{j}\) to \(w_{j}\).
We now show that \(T\) is a Linear Map. This part proof is just route algebra so I won’t type it again.
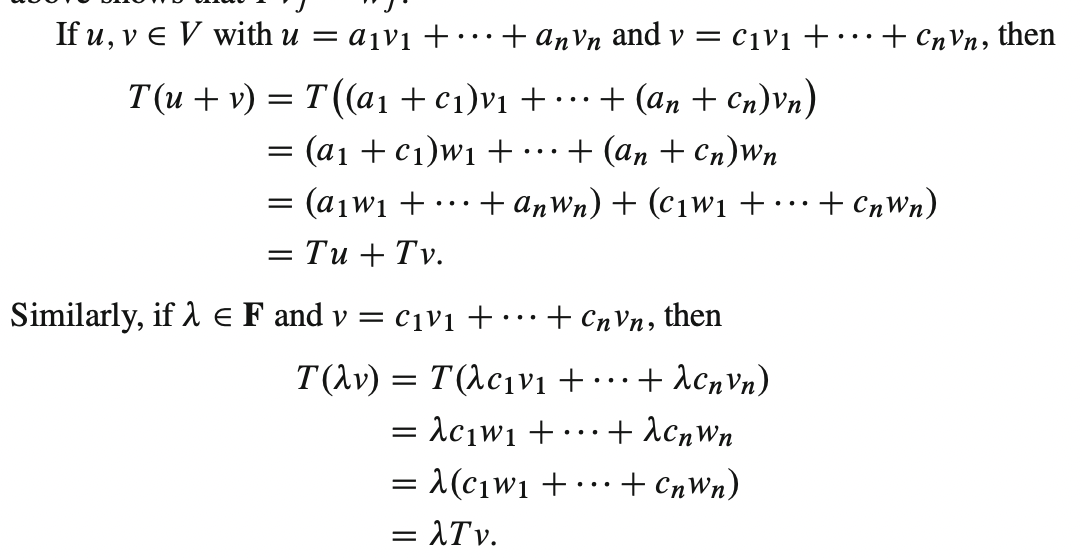
Uniqueness
Suppose there is a Linear Map that has the desired property: that \(T \in \mathcal{L}(V,W)\) and that \(Tv_{j}=w_{j}, \forall j=1, \dots n\). For any scalar \(c_{j}\), the homogeneity of \(T\) indicates that this same \(T\) has to take \(T(c_{j}v_{j}) = c_{j}Tv_{j} = c_{j}w_{j}\).
Now, the additivity of \(T\) also indicates that we can string these \(c_{j} v_{j}\) together in the same \(T\); that:
given \(T(c_{j}v_{j}) = c_{j}w_{j}\), we can just string it all together to get \(T(c_1v_1 + \dots + c_{n}v_{n}) = c_1w_1+ \dots + c_{n}w_{n}\).
This means that there is only one \(T\) that behaves in the way that we desire, on the span of \(v_1 \dots v_{n}\). Those vectors being the basis, their span is just the domain \(V\). This makes \(T\) uniquely determined on \(V\) as we were able to construct the original given map simply by following the rules of the Linear Map.