A Baysian Network is composed of:
- a directed, acyclic graph
- a set of conditional probabilities acting as factors.
You generally want arrows to go in the direction of causality.
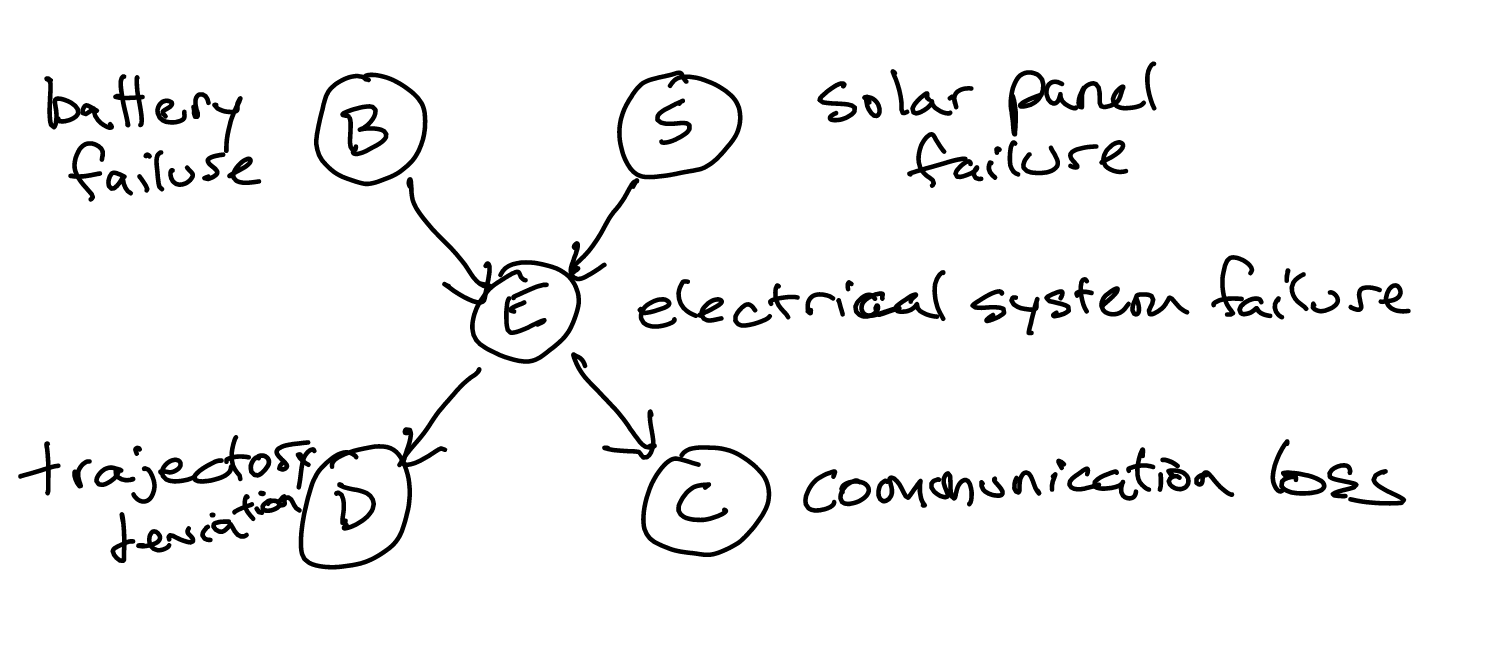
Via the chain rule of Bayes nets, we can write this equivalently as:
\begin{equation} (P(B) \cdot P(S)) \cdot P(E \mid B,S) \cdot P(D \mid E) \cdot P(C \mid E) \end{equation}
generally, for \(n\) different variables,
\begin{equation} \prod_{i=1}^{n} p(X_{i} \mid pa(x_{i})) \end{equation}
where, \(pa(x_{i})\) are the parent values of \(x_{i}\).
conditional independence
\(X\) and \(Y\) are conditionally independent given \(Z\) IFF:
\begin{equation} P(X, Y|Z) = P(X|Z) \cdot P(Y|Z) \end{equation}
(“two variables are conditionally independent if they exhibit independence conditioned on \(Z\)”)
this is equivalent to saying:
\begin{equation} P(X|Z) = P(X|Y,Z) \end{equation}
(“two variables are conditionally independent if the inclusion of the evidence of another set into the condition doesn’t influence the outcome if they are both conditioned on \(Z\)”)
We write:
\begin{equation} X \perp Y \mid Z \end{equation}
The network above has an important property: conditions \(B\) and \(S\) are independent; and conditions \(D\) and \(C\) are independent. Though they all depended on \(E\), each pair is conditionally independent.
checking for conditional independence
\((A \perp B \mid C)\) IFF ALL undirected paths from \(A\) to \(B\) on a Baysian Network exhibits d seperation, whose conditions are below:
A path is d-seperated by \(C\), the set of evidence if ANY of the following:
- the path contains a chain of nodes: \(X \to Y \to Z\) where \(Y \in C\)
- the path contains a fork: \(X \leftarrow C \to Z\), where \(Y \in C\)
- the path contains a inverted fork: \(X \to Y \leftarrow Z\), where \(Y\) is not in \(C\) and no descendent of \(Y\) is in \(C\).
Note that \(C\) can be empty. This is why, \(B,S\) is conditionally independent on nothing on that graph above, so they are just actually independent.
If the structure does not imply conditional independence, it does NOT mean that the structure is conditionally dependent. It could still be conditionally independent. end{equation}
markov blanket
the markov blanket of node \(X\) is the minimal set of nodes on a Baysian Network which renders \(X\) conditionally independent from all other nodes not in the blanket.
It includes, at most:
- node’s parenst
- node’s chlidren
- other parents of node’s children
Check that you need all of these values: frequently, you don’t—simply selecting a subset of this often d-seperates the node from everyone else.
parameter learning in Baysian Network
Let:
- \(x_{1:n}\) be variables
- \(o_1, …, o_{m}\) be the \(m\) observations we took
- \(G\) is the graph
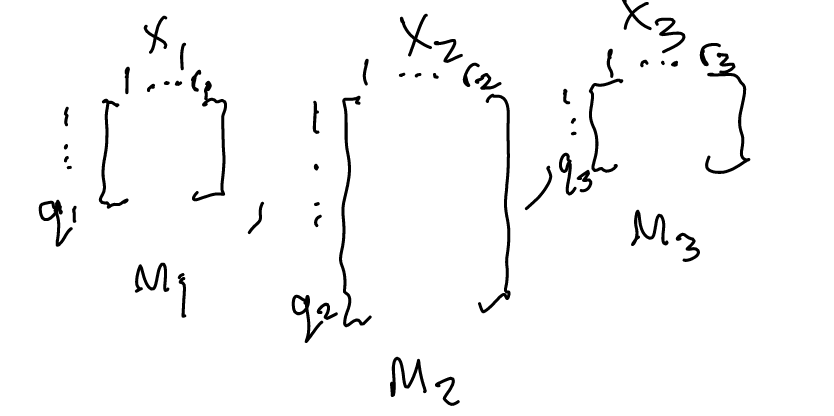
- \(r_{i}\) is the number of instantiations in \(X_{i}\) (for boolean variables, this would be \(2\))
- \(q_{i}\) is the number of parental instantiations of \(X_{i}\) (if parent 1 can take on 10 values, parent 2 can take 3 values, then child’s \(q_{i}=10\cdot 3=30\)) — if a node has no parents it has a \(q_{i}\) is \(1\)
- \(\pi_{i,j}\) is \(j\) instantiation of parents of \(x_{i}\) (the \(j\) th combinator)
What we want to learn from the graph, is:
\begin{equation} P(x_{i}=k | \pi_{i,j}) = \theta_{i,j,k} \end{equation}
“what’s the probability that \(x_{i}\) takes on value \(k\), given the state of \(x_{i}\)’s parents are \(\pi_{i,j}\) right now?”
Let us first make some observations. We use \(m_{i,j,k}\) to denote the COUNT of the number of times \(x_{i}\) took a value \(k\) when \(x_{i}\) parents took instantiation \(j\). This is usually represented programmatically as a set of matrices:
To learn the parameter as desired, we use:
\begin{equation} MLE\ \hat{\theta}_{i,j,k} = \frac{m_{i,j,k}}{\sum_{k’} m_{i,j,k’}} \end{equation}
In that: we want to sum up all possible value \(x_{i}\) takes on, and check how many times it takes on a certain value, given the conditions are the same.