bit
A computer is built out of binary gates:
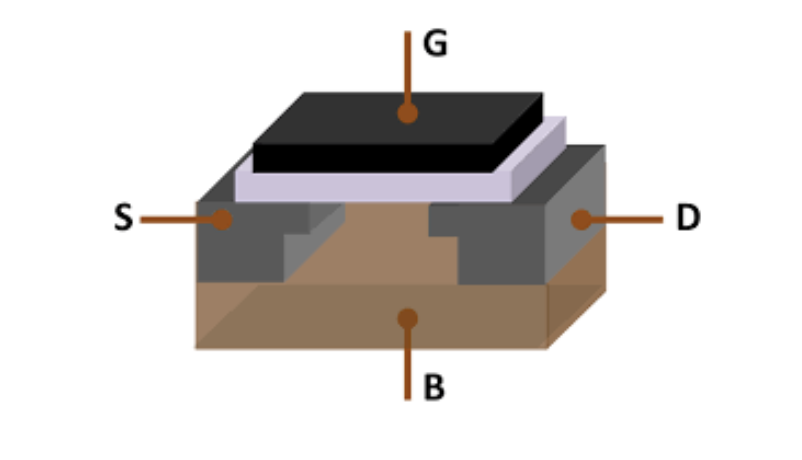
So, having voltage into \(B\) allows current to pass through between \(S\) and \(D\), it could be on/off.
byte
Accumulation of \(8\) bits
Computer memory is a large array of bytes. It is only BYTE ADDRESSABLE: you can’t address a bit in isolation.
bases
Generate, each base uses digits \(0\) to \(base-1\).
We prefix 0x to represent hexadecimal, and 0b to represent binary.
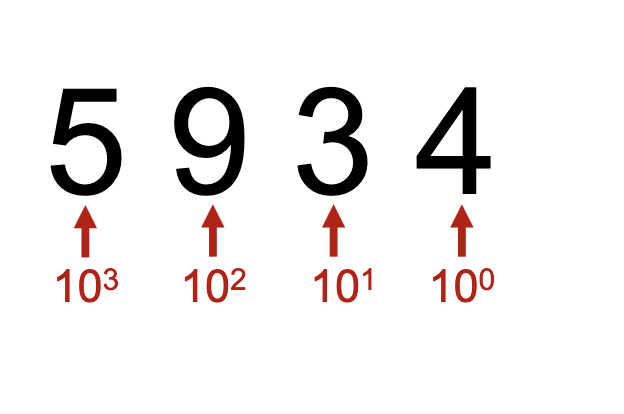
base 10
base 10 uses digits \(0-9\). Each place value represents to a certain power of \(10\): \(10^{n}\) at each place value \(n\), starting at \(0\).
base 2
base 2 uses digits \(0-1\). Each place value represents a certain power of \(2\): \(2^{n}\) at each place \(n\), starting at \(0\).
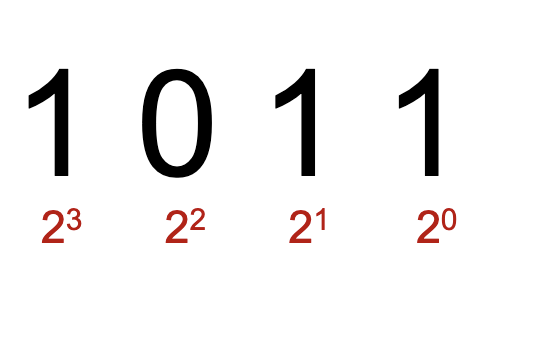
The leftmost (largest value) is considered most-significant bit, right most is the least-significant bit.
conversion from base 10 to base 2
“What is \(6\) is base 2?”
- What’s the largest power of \(2 \leq 6\)? Well, we have \(2^{2}\). Therefore, the first place value is \(2\), which is the third digit.
- now, we subtract the remainder, we now have \(6-4=2\) , which is \(2^{1}\)
min and max of binary
The maximum value could be one minus the extra place value. For instance, if you have \(8\) digits (i.e. 7 place values), you would only be able to represent:
\begin{equation} 2^{8}-1 = 255 \end{equation}
multiplying and dividing by base
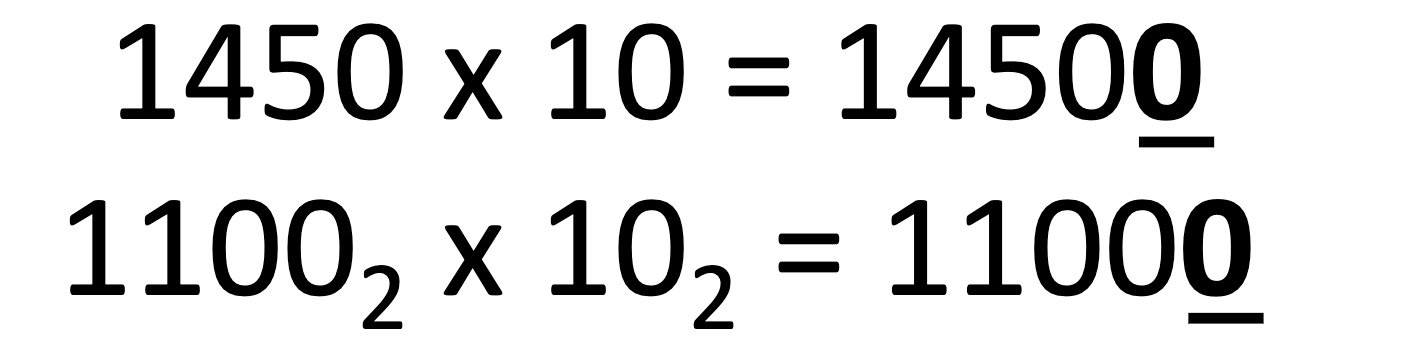
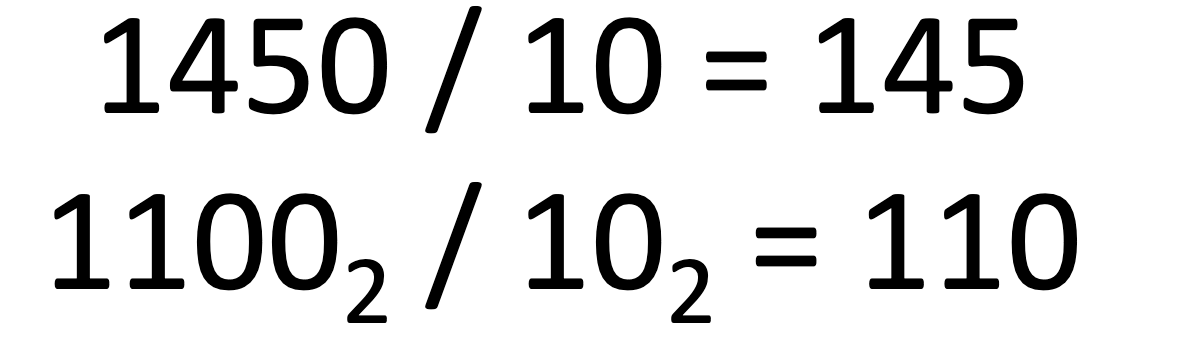
It works in the way you expect.
base 16
We can use base 16 essentially to divide base 2 numbers into groups of \(4\).
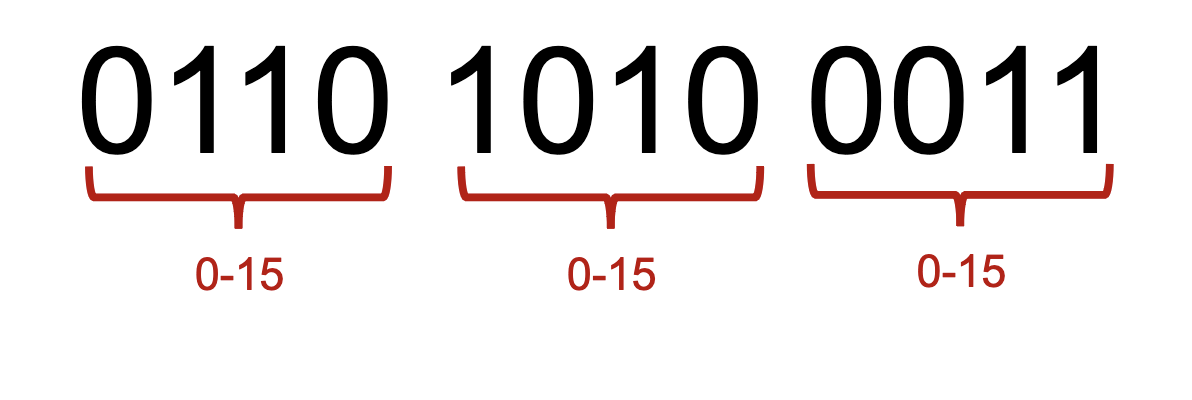
Each quartet of bits can be converted separately
“Which bit is missing”
The way you can do conversion in your head more simply is to stare at a binary number in groups of \(4\), and see which missing bytes are there and subtract that much.
numerical representations
unsigned integers
Positive numbers and 0. A number is either \(0\) or some positive integer.
The range of is \(2^{w}-1\) where \(w\) is the number of bits, because we are cramming the entire number from \(0\) to \(2^{w}-1\).
signed integers
Negative, positive, and \(0\).
a bad system

The fact that \(0\) is signed is quite bad. And like adding negative numbers to positive number is very hard because you need another processor to figure out what the sign is.
two’s complement
sizes of stuff
(bytes)

- int: 4
- float: 4
- double: 8
- char: 1
- pointer: 8 (for 64 bit systems)
- short: 2
- long: 8
overflow
If you exceed the maximum value of bit representation, it rolls over to becoming negative. If you subtract one, you have to borrow from an imaginary