A binomial distribution is a typo of distribution whose contents are:
- Binary
- Independent
- Fixed number
- Same probability: “That means: WITH REPLACEMENT”
Think: “what’s the probability of \(n\) coin flips getting \(k\) heads given the head’s probability is \(p\)”.
constituents
We write:
\begin{equation} X \sim Bin(n,p) \end{equation}
where, \(n\) is the number of trials, \(p\) is the probability of success on each trial.
requirements
Here is the probability mass function:
\begin{equation} P(X=k) = {n \choose k} p^{k}(1-p)^{n-k} \end{equation}
additional information
properties of binomial distribution
- expected value: \(np\)
- variance: \(np(1-p)\)
deriving the expectation
The expectation of the binomial distribution is derivable from the fact:
\begin{equation} X = \sum_{i=1}^{n} Y_{i} \end{equation}
where,
\begin{equation} \begin{cases} X \sim Bin(n,p) \\ Y_{i} \sim Bern(p) \end{cases} \end{equation}
Now, recall that expected value is linear.
Therefore, we can write that:
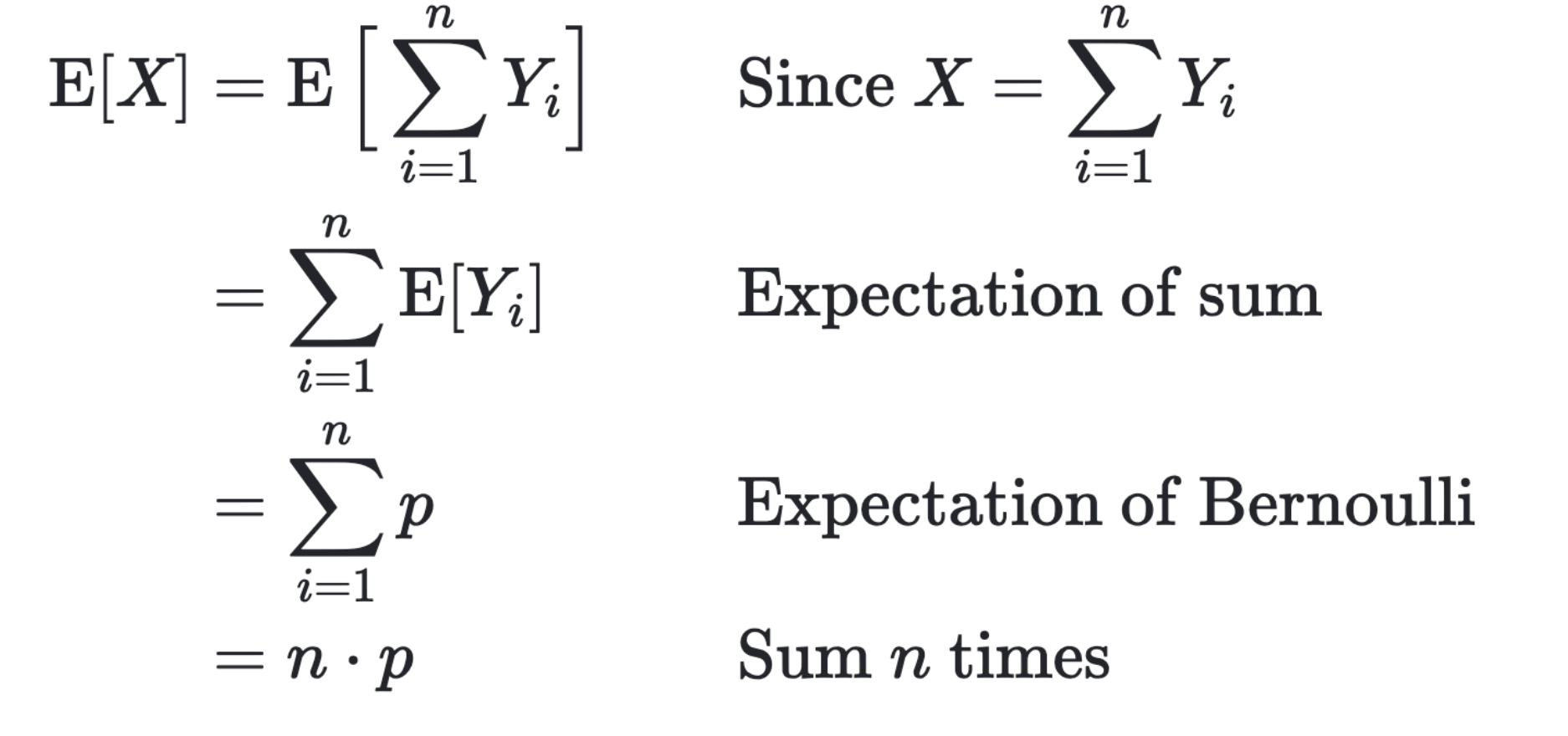
approximating binomial
- normal distribution approximation: \(n > 20\), variance large \((np(1-p)) > 10\), absolute independence; beware of continuity correction
- poisson distribution approximation: \(n > 20\), p small \(p < 0.05\)
adding binomial distribution
For \(X\) and \(Y\) independent binomial distributions, with equivalent probability:
\begin{equation} X \sim Bin(a, p), Y \sim Bin(b, p) \end{equation}
Then:
\begin{equation} X+Y \sim Bin(a+b, p) \end{equation}