We have a function:
\begin{equation} |x|+|y|\frac{dy}{dx} = \sin \left(\frac{x}{n}\right) \end{equation}
We are to attempt to express the solution analytically and also approximate them.
To develop a basic approximate solution, we will leverage a recursive simulation approach.
We first set a constant \(N\) which in the \(N\) value which we will eventually vary.
N = 0.5
We can get some values by stepping through \(x\) and \(y\) through which we can then figure \(\frac{dy}{dx}\), namely, how the function evolves.
# cache
res = []
# number of steps
steps = 1000
# seed values
x = -5
y = 5
# step size
step = 1/100
# for number of setps
for _ in range(steps):
# get the current equation and slope solution
dydx = (sin(x/N)-abs(x))/abs(y)
# append result
res.append((x,y,dydx))
# apply the slope solution to iterate next y
# step size is defined by `step`
x += step
y += dydx*step
We have now a set of analytic solutions \((x,y,\frac{dy}{dx})\). Let’s plot them!
scatter_plot([i[0:2] for i in res])
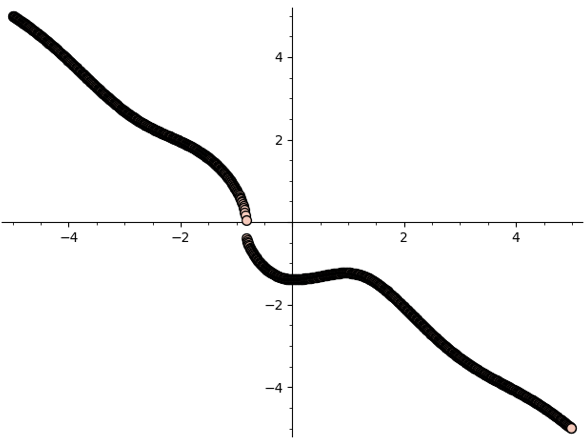
Great, now we have a fairly non-specific but “correct” solution. We are now going to try to derive an analytic solution.
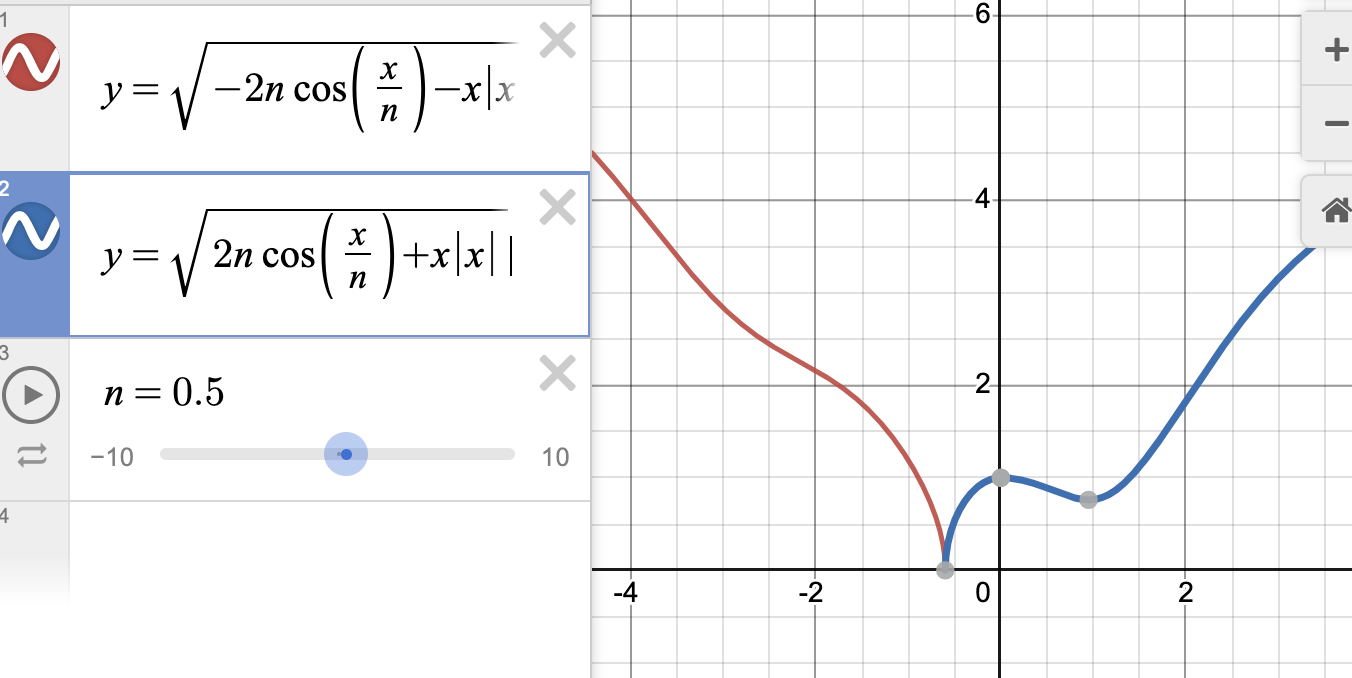
Wait… That’s not the solution we got! But… its close: the blue line simply need to be reflected across the \(x\) axis.
Its actually fairly apparent why we will need this negative. We just declared that \(y\) was negative for that portion of the solution; the output of a square root could never be negative, so of course to achieve \(y\) being negative we have to take into account that square roots have a possible negative output as well.
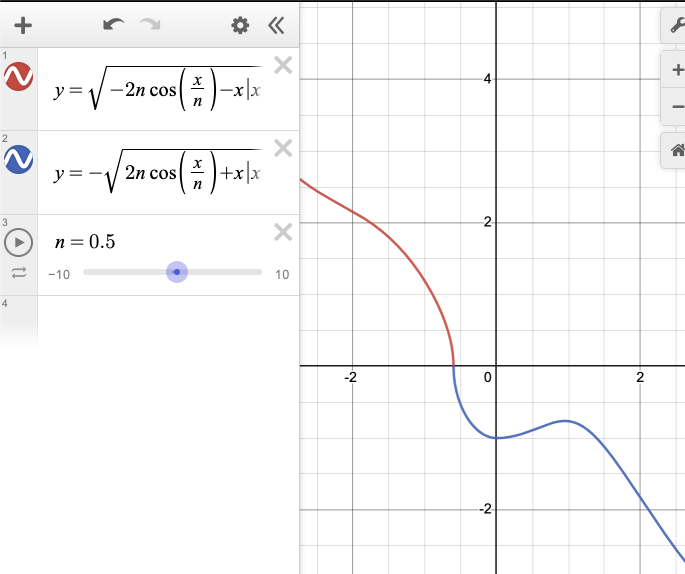
Nice; now our analytical results agree with out numerical results.
\begin{equation} \begin{cases} y>0 & y=\sqrt{-2n\cos\left(\frac{x}{n}\right)-x\vert x\vert} +C \\ y<0 & y=-\sqrt{2n\cos\left(\frac{x}{n}\right)+x\vert x\vert}+C \end{cases} \end{equation}
Moving on to the result of the questions.
Solution behavior
The solution are unbounded and mostly decreasing. As \(n\in [-1,1]\), the solution becomes unstable; a solution does not exist at \(n=0\).
At \(n=0.5\), a solution passes through \((0,-1)\).