conditional plan is a POMDP representation technique. We can represent a conditional plan as a tree.
toy problem
crying baby POMDP problem:
- actions: feed, ignore
- reward: if hungry, negative reward
- state: two states: is the baby hungry or not
- observation: noisy crying (she maybe crying because she’s genuinely hungry or crying just for kicks)
formulate a conditional plan
we can create a conditional plan by generating a exponential tree based on the observations. This is a policy which tells you what you should do given the sequence of observations you get, with no knowledge of the underlying state.
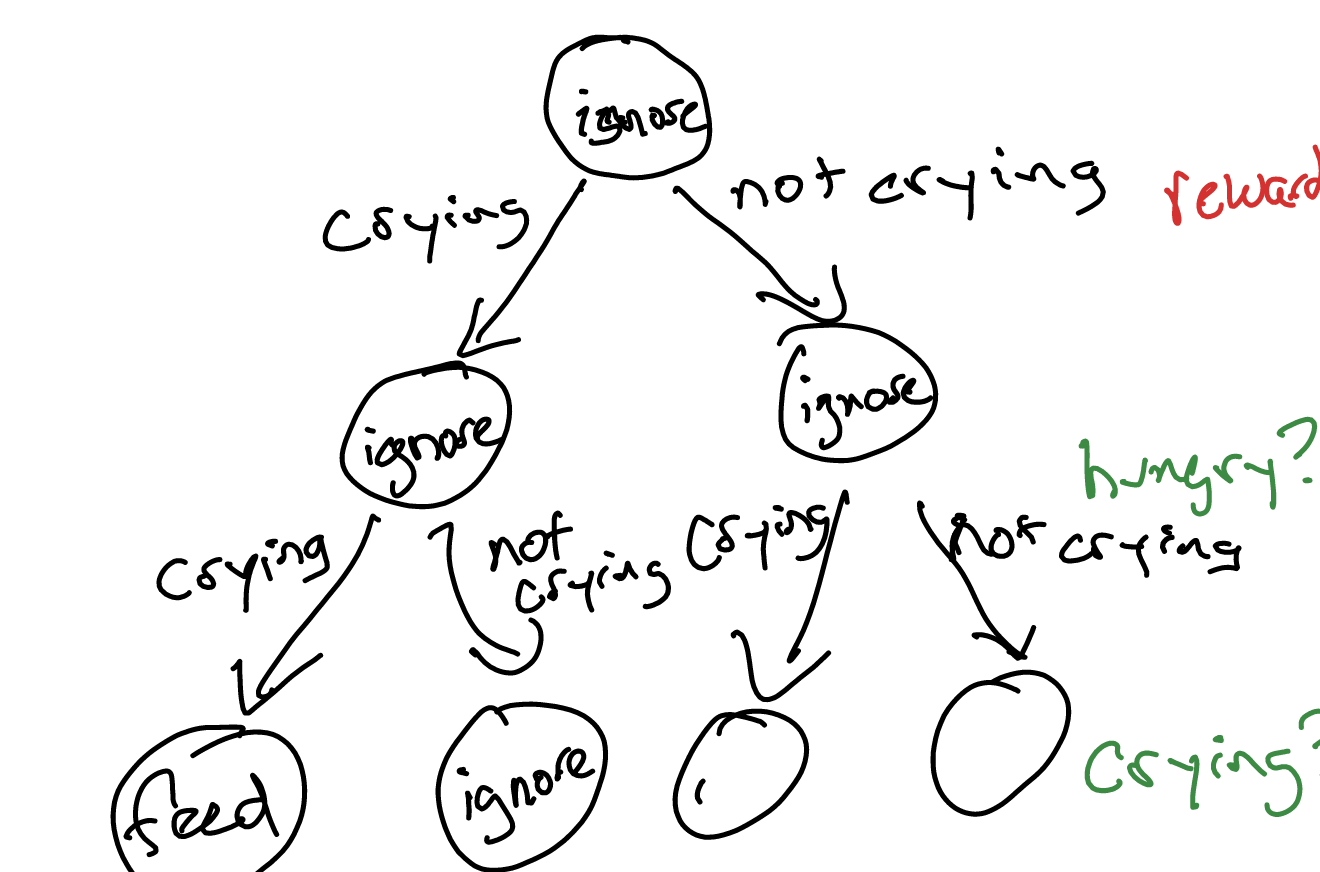
We call this plan \(\pi\) (shock suprise). We define two notations:
- \(\pi()\): the ACTION at the head of this tree (in this case, “ignore”)
- \(\pi(o)\): the SUBTREE which is one-level below the first action. For instance, for both observations of the tree above, \(\pi(o)()\) is ignore for both \(o\).
conditional plan evaluation
Assume we have a starting at some given true state \(s\). We can evaluate a conditional plan at that state by formulating:
\begin{equation} U^{\pi} (s) = R(s, \pi()) + \gamma \qty[\sum_{s’} T(s’|s, \pi()) \sum_{o} O(o|\pi(), s’) U^{\pi(o)}(s’)] \end{equation}
where, \(\pi()\) is the action at the root node of the tree; and \(\pi(o)\) is the subtree for subplan at observation \(o\); essentially, at each point where we evaluate \(U\), we move the root node forward and recalculate. If we run out of depth, the utility is \(0\) and hence the whole right term is \(0\).
Of course this assumes we know what our initial state is. Which is lame. So now:
\begin{equation} U^{\pi}(b) = \sum_{s}^{} b(s) U^{\pi}(s) \end{equation}
which will give us the utility of our policy given a belief about wher ewe are.
so literally take our belief about the probability of us being in each initial state and calculate it for each of our initial states.
optimal value function for POMDP
\begin{equation} U^{*}(b) = \max_{\pi} U^{\pi}(b) \end{equation}
Of course, trying to actually do this is impossible because you have to iterate over all possible policies and then calculate every utility from them.
This is practically untenable, because the space of \(\pi\) is wayyy too big. Hence, we turn to alpha vectors.