Could a different choice of evaluation order change the terminating result of the program; note that this says nothing about whether or not particular evaluation order terminates.
constituents
requirements
A set of rewrite rules is confluent if for any expression \(E_0\), should \(E_0 \to^{* } E_1\) and \(E_0 \to^{* } E_2\), then there exists some \(E_3\) such that \(E_1 \to^{*} E_3\) and \(E_2 \to^{ *} E_3\)
Why this instead of saying we will end up at one state after all evaluations? Suppose a particular system never terminates, we have to specify a particular confluent state because otherwise the notion of all is bad.
additional information
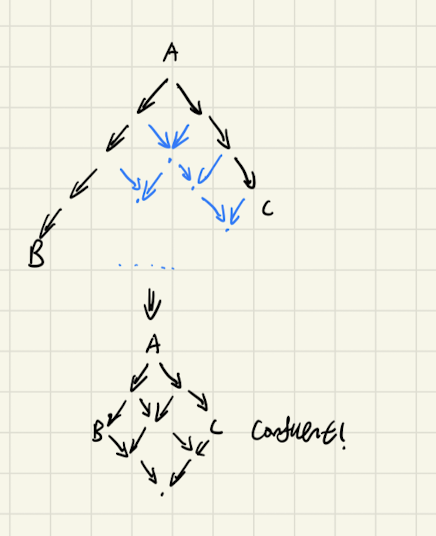
one-step diamond property
if for all \(A\), \(A\to B\) and \(A \to C\) implies that there exists some \(D\) such that \(B \to D\) and \(C \to D\), this system exhibit a one-step diamond property.
If some system has one-step diamond property, then that system is confluent. This is a sufficient but not necessary property.
Proof: induction
go build a grid using the one step diamond property
SKI exhibits one-step diamond property
We can’t naively apply one-step diamond property.
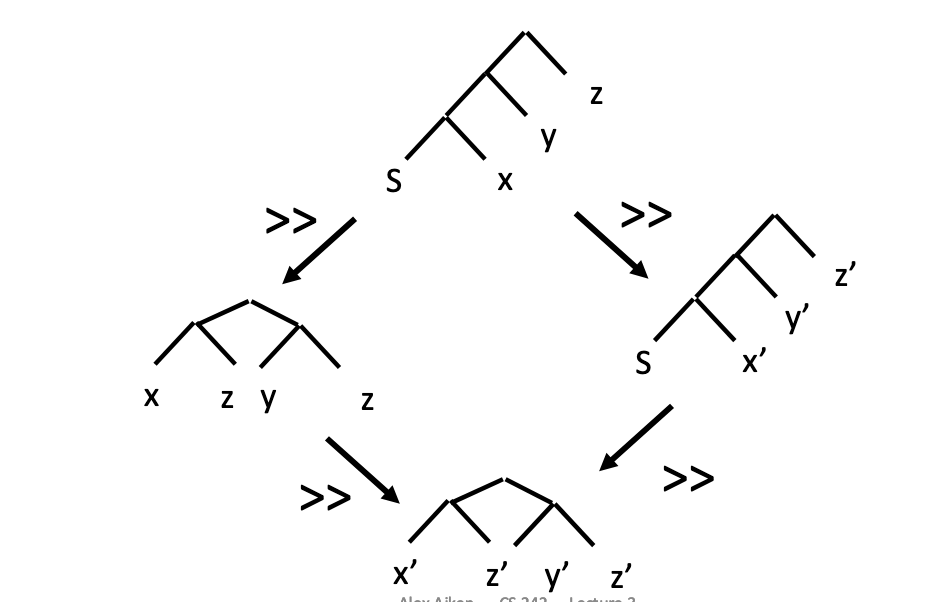
We have to first define a new relation \(\gg\) for SKI Calculus, which deals with the fact that \(Sxyz \to (xz) (yz) \to (xz’) (yz’)\) isn’t one step because expanding \(z\) before and after results in a different number steps.
we define \(X \gg Y\), if…
- \(X \to Y\) via a rewrite at the root node
- \(X = A B, Y = A’ B’\) and \(A \gg A’\), \(B \gg B’\)
we allow multiple rewrites if they are in independent subtrees

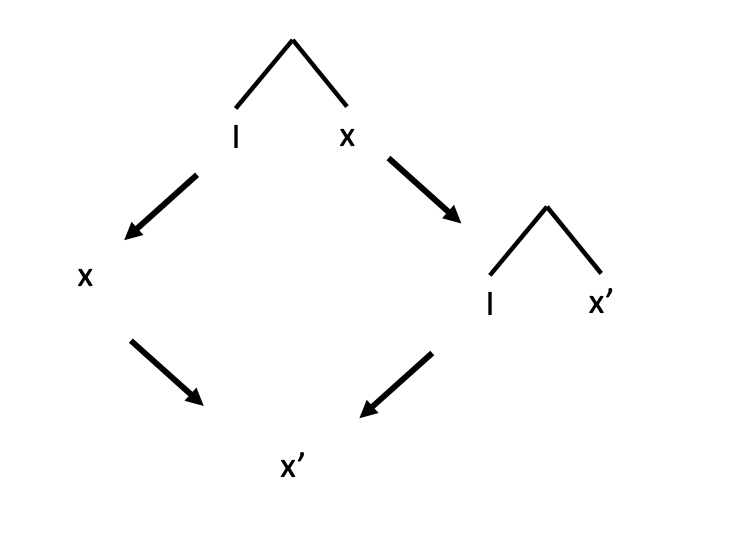
Ix
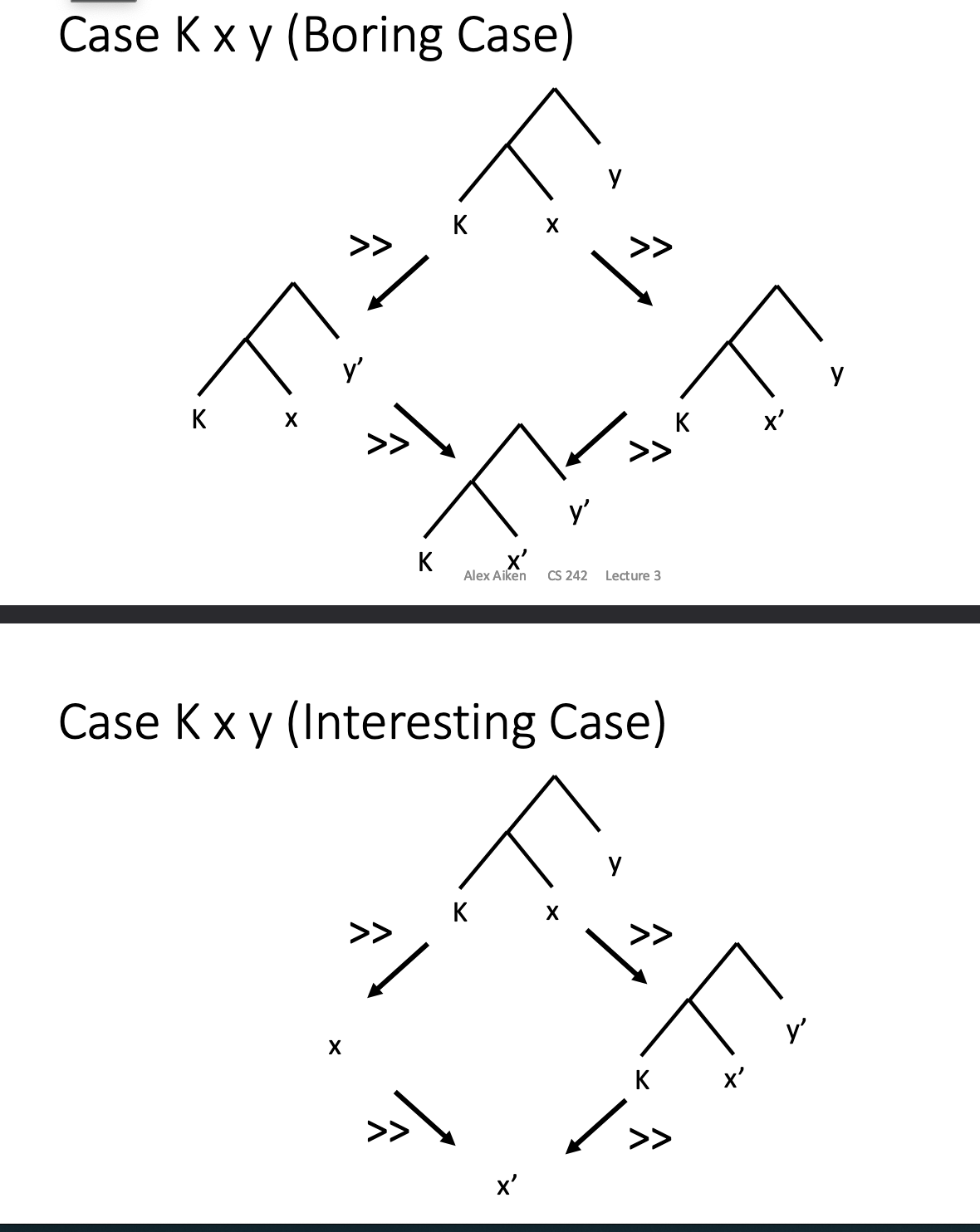
Kxy
Sxyz