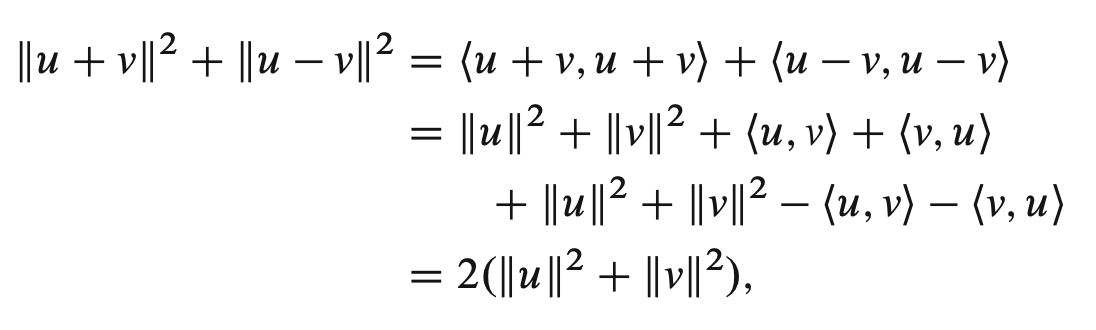Pythagorean Theorem
\begin{equation} \|u + v\|^{2} = \|u \|^{2} + \|v\|^{2} \end{equation}
if \(v\) and \(u\) are orthogonal vectors.
Proof:
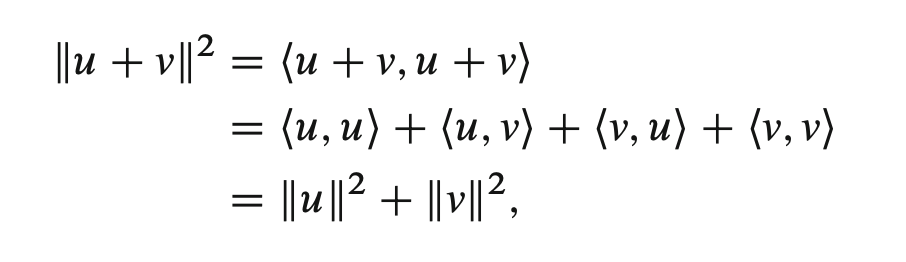
An Useful Orthogonal Decomposition
Suppose we have a vector \(u\), and another \(v\), both belonging to \(V\). We can decompose \(u\) as a sum of two vectors given a choice of \(v\): one a scalar multiple of \(v\), and another orthogonal to \(v\).
That is: we can write \(u = cv + w\), where \(c \in \mathbb{F}\) and \(w \in V\), such that \(\langle w,v \rangle = 0\).
Here’s how:
For nonzero \(v\)
\begin{equation} c = \frac{\langle u,v \rangle}{\|v\|^{2}} \end{equation}
and
\begin{equation} w = (u - cv) \end{equation}
We can show \(\langle w,v \rangle=0\) as follows:
\begin{align} \langle (u-cv), v \rangle &= \langle u,v \rangle - \langle cv, v \rangle \\ &= \langle u,v \rangle - c \langle v,v \rangle \\ &= \langle u,v \rangle - \frac{\langle u,v \rangle}{\|v\|^{2}} \langle v,v \rangle \\ &= \langle u,v \rangle - \frac{\langle u,v \rangle}{\|v\|^{2}} \|v\|^{2} \\ &= 0 \end{align}
Cauchy-Schwartz Inequality
\begin{equation} | \langle u,v \rangle | \leq \|u\| \|v\| \end{equation}
and the expression is an equality of each vector \(u,v\) is the scalar multiple of the other.
Proof:
Pick some set of \(v\) and \(u\) and write out the orthogonal decomposition we had outlined above:
\begin{equation} u = cv + w \end{equation}
Now, recall \(c = \frac{\langle u,v \rangle}{\|v\|^{2}}\). We now apply Pythagorean Theorem:
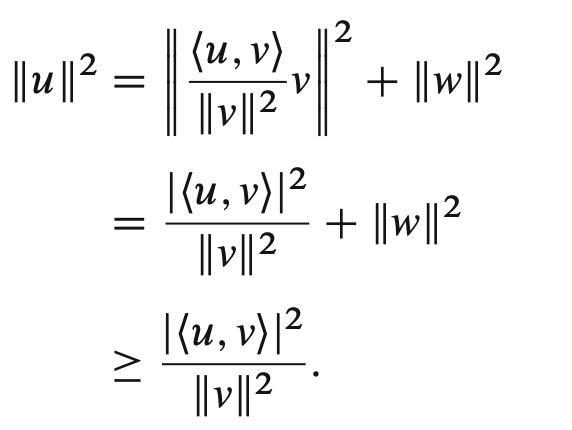
Now we just multiply \(\|v\|^{2}\) to both sides and take square roots.
If \(w = 0\) (i.e. \(v\) and \(w\) have no othogonal component, and therefore they are scalar multiples), then this would turn into an equality as desired.
triangle inequality (vectors)
See also triangle inequality (complexes)
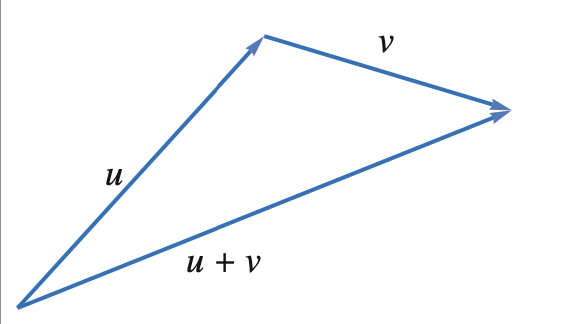
“The length of \(u+v\) is always less than the length of each \(u\) plus \(v\); the third side length is always shorter than the sum of both other sides’ lengths.”
\begin{equation} \|u\| + \|v\| \geq \|u+v\| \end{equation}
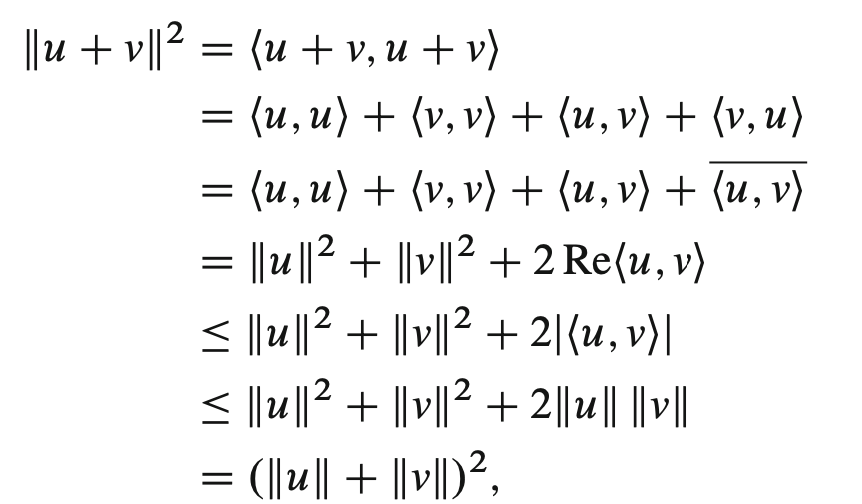
Notably, the two lines between \(2|\langle u,v \rangle|\) and \(2 \|u\| \|v\|\) holds because of the Cauchy-Schwartz Inequality.
This inequality becomes an equality if \(u\) and \(v\) are a non-negative multiple of the other.
parallelogram equality
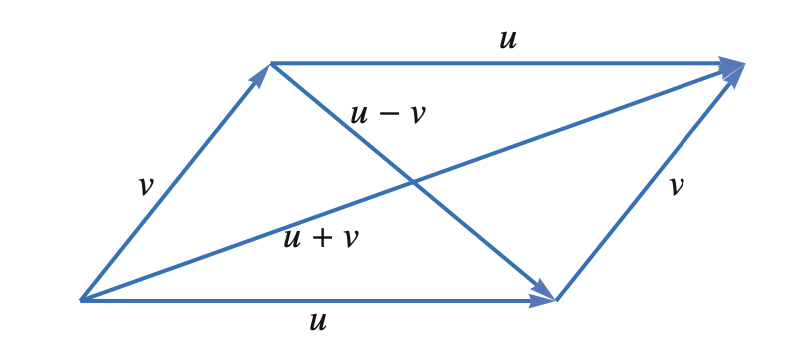
The sums of squared side lengths of a parallelogram is equal to the sum of the squares of the length of diagonals:
\begin{equation} \|u + v\|^{2} + \|u-v\|^{2} = 2(\|u\|^{2} + \|v\|^{2}) \end{equation}