crap to remember for AP Stats is a cram sheet for the AP Statistics exam.
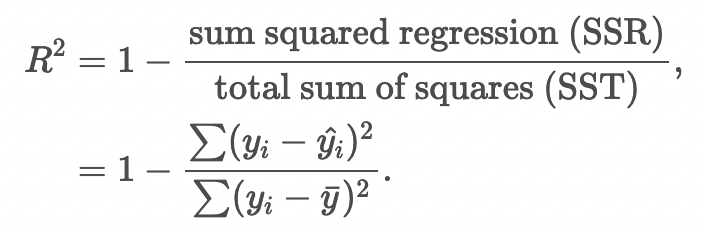
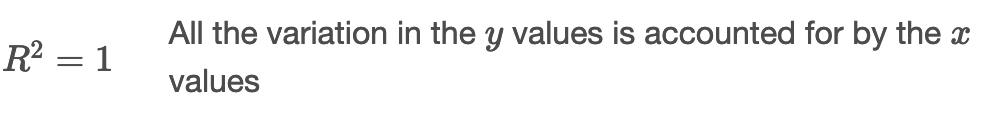

95% confidence: \(z^*=1.96\)
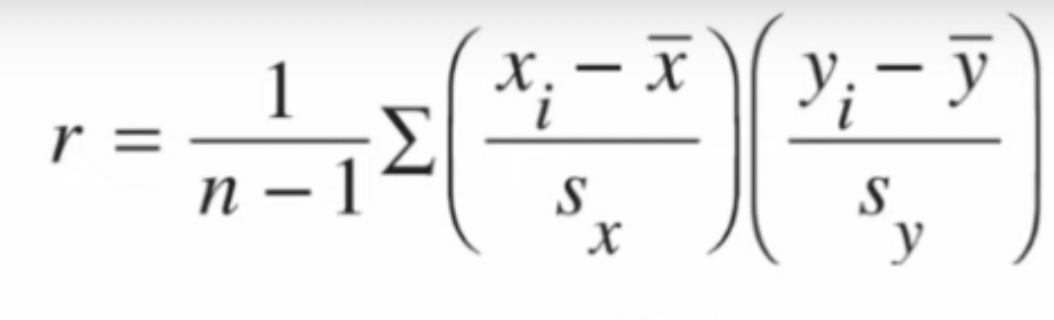
- \(r=1\): perfect positive correlation
- \(r=-1\): perfect negative correlation
- \(r=0\): no correlation
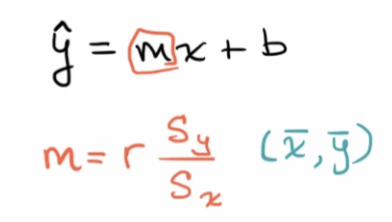

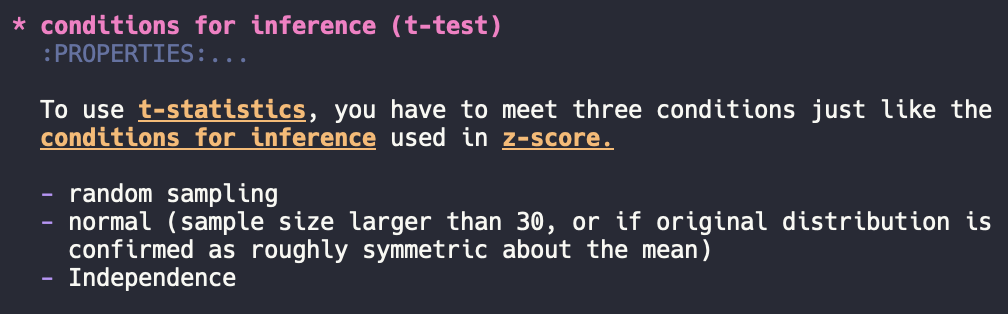



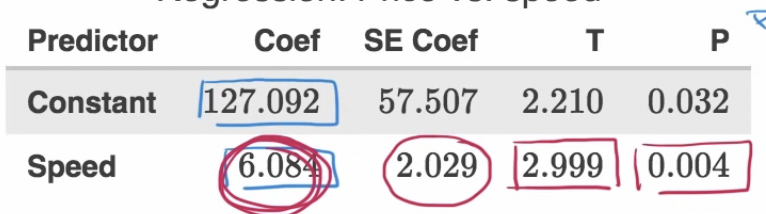
- S: standard deviation of residuals
- R-sq: how much of varience in dep. var can be explained by indp. var
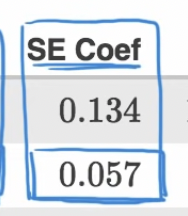
SE: estimate of standard deviation of the random var. that is slope.
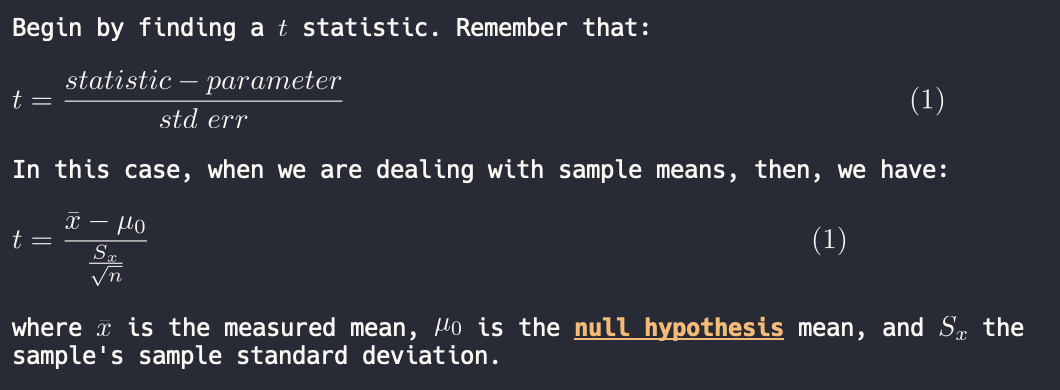
For lines:
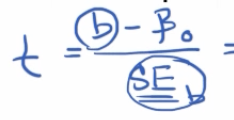
Note that p value from regression outputs are two-tailed. So divide by 2 if you want a one-tail result.
Multiplication changes mean as well as well as standard deviation. Adding changes mean but not standard deviation.
Expected value of the sum and differences of random variables are just the sums and differences of their expected value. \(S = X+Y, \bar{S} = \bar{X}+\bar{Y}\).
Variance of random variables are just the sum and differences of their variance. \(S=X+Y,{\sigma^2}_S = {\sigma^2}_X+{\sigma^2}_Y\).
#WHAPS
- what test
- what hypothesis and what significance level
- assumptions and conditions; state!
- random
- independent: \(\le 10\%\) of population.
- t and z special: normal (z tests: \(np, n(1-p) \geq 10\), t tests: \(n>30\) or given)
- chi-square special: \(\forall\ EV > 5\)
- p: z-statistic that would

XD: Control (control for confounding and bias, placebo, etc.), Randomization (spread uncontrolled variability), Replication (need to have adequate units and ability to be repeated)

=> Describing a distribution
- Center: Mean, Median, or Mode? figure by skew
- Shape: Symmetric vs Skewed? Unimodal vs Bimodal
- Spread: Range and Inter-Quartile Range
- Outlier: anything more than 1.5*IQR away
- Context: what the distribution shows
“Experimental Unit”: a physic entity that’s the primary unit of interest in a research objective.
Conditions for binomial distribution:
- Binary
- Independent
- Fixed number of trials
- All trials with same probability
Conditions for geometric distrubiton
- Binary
- Independent
- Fixed number of successes
- All trials with same probability
state the thing, state the conditions: “normal distribution with n= s=”, binomial distribution with n= p= etc.