key idea: let’s build a tree such that, after taking the action, the observation is deterministic. Therefore, you get a belief tree with no branching on observations.
DESPOT trees
We make an assumption, that the actual observation given are fixed given belief. That is:
\begin{equation} O(o|b,a) = 1 \end{equation}
for some specific \(o\), everything else is \(0\) for every b,a.
Sample Scenarios
To make such a tree, let’s sample of set of scenarios: sequences of actions and observations (because, given a belief and action, we assume observation is fixed. So, given an initial belief and an action, you will always go down a single “scenario”).
Build Tree
Do a bunch of scenario sampling
Use Tree
Starting at where you are in terms of initial belief, greedily choose the “best action”.
Evaluate Tree
Average discounted future reward of the scenarios that relate to your starting states.
Drawbacks
Normal DESPOT is very very easy to overfit.
Regularized DESPOT
Build a DESPOT until depth \(D\), with \(K\) senarios, then, treat the resulting tree as a conditional plan, do bottom-up DP to optimize the plan.
Given a set of senarios \(\Phi\), we write:
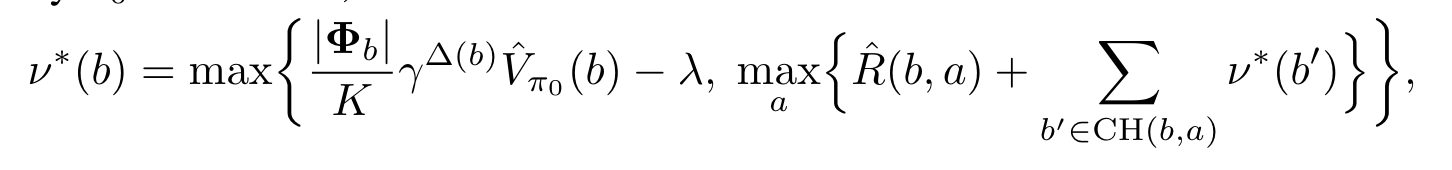
Anytime DESPOT
We build up the despot tree by maintaining upper and lower bounds on the value function, and try to expand on scenarios that would help us lower the gap between them.
First, pick an upper and lower bound. The note on HSVI may help.
- Build and Optimize Bounded DESPOT tree (see below) starting at \(b_{0}\)
- Compute the optimal policy using Regularized DESPOT expression above
- Execute best action
- Get observation
- \(update(b,a,o)\)
Building Bounded DESPOT
- sample a set of \(\Phi\) senarios at \(b_0\)
- insert \(b_0\) into the tree as the root node
- let \(b \leftarrow b_0\), and, as time permits:
- tighten bounds on \(b\)
- back up the upper and lower bounds you found all the way up the tree as you would with HSVI
Tightening Bounds
if \(b\) is a leaf on the tree, then add new belief nodes for every action and every observation as children of \(b\).
then,
\begin{equation} b \leftarrow update(b, a^{*}, o^{*}) \end{equation}
where \(a^{*}\) and \(o^{*}\) are determined by…
- \(a^{*}\): IE-MAX Heuristic, where the original upper-bound is \(Q\)
- \(o^{*}\): weighted excess uncertainty
If the weighted excess uncertainty we got is non-zero, we repeat this tightening bounds process until it is zero.
DESPOT Theoretic Guarantees
It is near-optimal as a policy.