Computational memory of this type of model is fixed. In particular, the class of problems this type of automata solves (“languages it recognizes”) is called regular languages.
We want to explore the closure properties of regular languages (does combining regular languages result in regular languages)
constituents
A DFA is a five-tuple \(M = (Q, \Sigma, \delta, q_{0}, F)\).
- \(Q\): finite set of all states
- \(\Sigma\): the alphabet
- \(\delta: Q \times \Sigma \to Q\), the transition function
- \(q_0 \in Q\): the start state
- \(F \subseteq Q\): the accept states, which means we accept the input string we got if after processing the string we ended up at one of these states
requirements
if processing an input results in an accepting state, we accept the input; otherwise, we reject the input. this is the computation.
accept
Let \(w_1, …, w_{n} \in \Sigma\), and \(w = w_1 … w_{n} \in \Sigma^{*}\), \(M\) accepts \(w\) if there exists \(r_0, …, r_{n} \in Q\) such that:
- \(r_{0} = q_{0}\)
- \(\delta(r_{i}, w_{i+1}) = r_{i+1}\) for all \(i=0, …, n-{1}\), and
- \(r_{n} \in F\)
additional information
L(M)
the set of all strings that \(M\) accepts is called the “language recognized by \(M\)”, or “the function computed by \(M\)”.
important factoid: empty language is not the empty string, the empty language contains no strings, the empty string contains no content, which means you stay at \(q_0\)
regular language
see regular language
DFAs are equivalent to NFAs
see DFAs are equivalent to NFAs
DFAs recognize the same set of languages as NFAs, that is, regular languages.
regular expressions
examples and factoids
why DFAs?
- constant size memory => important, dynamically adding memory does bring more computational power
- read input once => unimportant, being able to go back and fourth doesn’t add additional computational power
original introduction of nondeterminism
Limitations of DFAs
- pumping lemma
- Myhill-Nerode (entire characterization of regular languages)
simple things to make and do with DFAs because they are so simple
- optimize DFA: for a given regular language, what is the smallest DFA?
- learning DFA
examples
proof: this language accepts an odd number of \(1\)
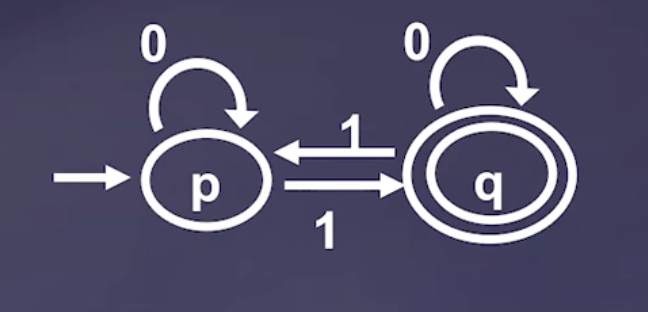
We show this by induction on the string length.
- base, this string has zero length, and we reject the string
- suppose for a string of length \(n\), \(M\) accepts \(n\) IFF \(n\) has an odd number of \(1\)
- now, consider a string of length \(n+1\), casework:
- we are at an accept state, and we got a \(0\): this means we still have an odd number of \(1\), we don’t go anywhere, we can accept
- we are at an reject state, and we got a \(1\): this means we now have an odd number of \(1\), we go to \(q\), and we can accept
- ….
build a DFA that accepts at least strings that contain \(001\)
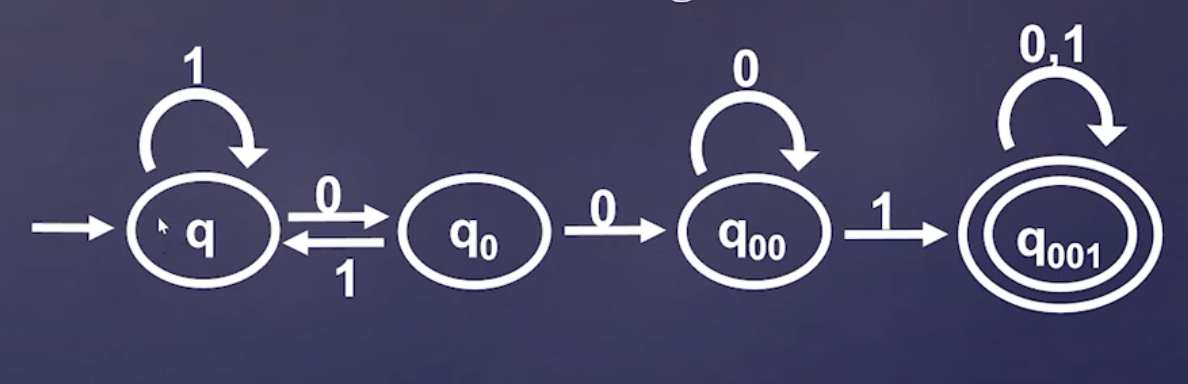
this requires some thinking, and the trick is simply keeping track of what you saw in the states, and if you saw something contradictory backtrak if needed
constructing a binary addition system
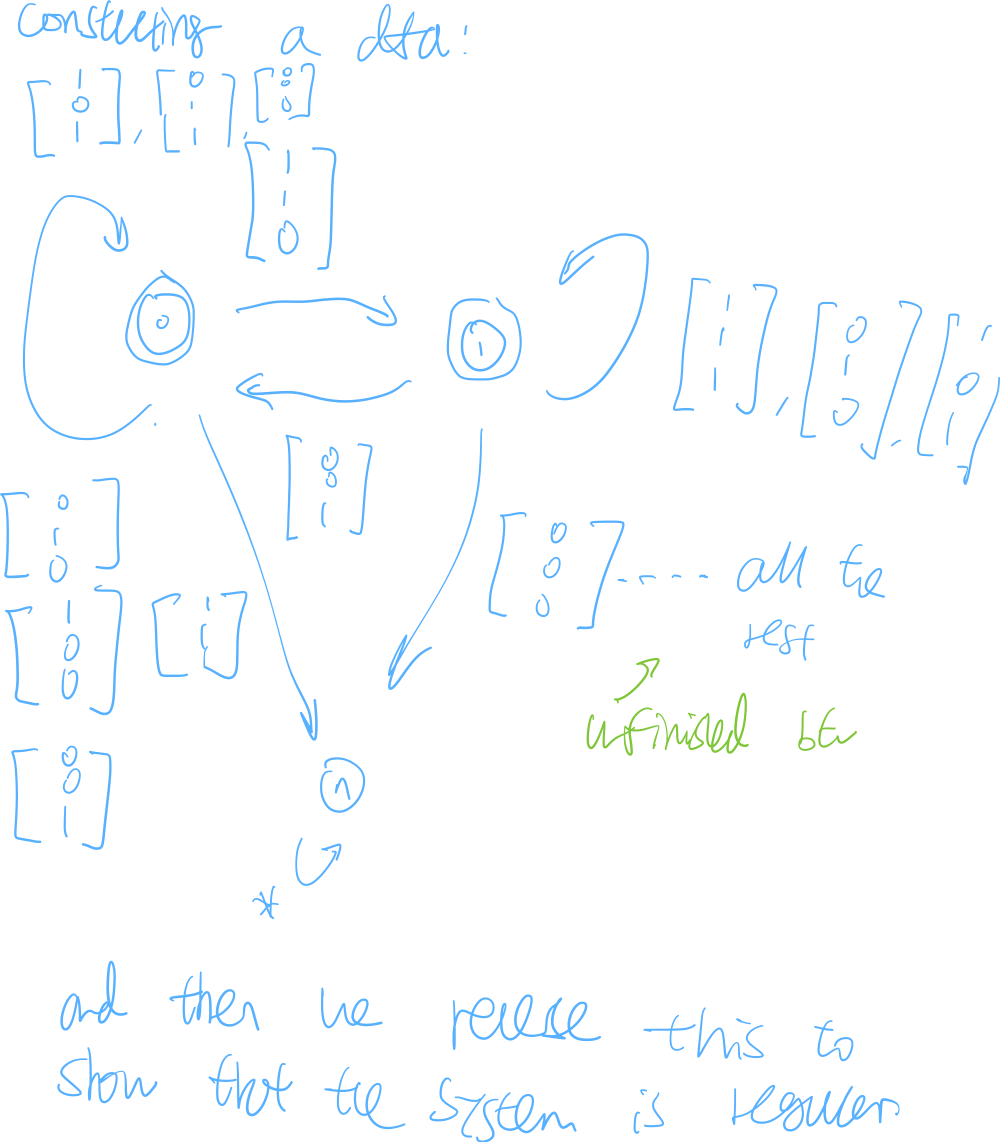
pumping lemma
see pumping lemma
Minimizing DFAs
see Minimizing DFAs
Learning DFA
See PAC Learning