Diagonal Matrix

The diagonal of a square matrix consists of entries from the upper-left to the bottom-right

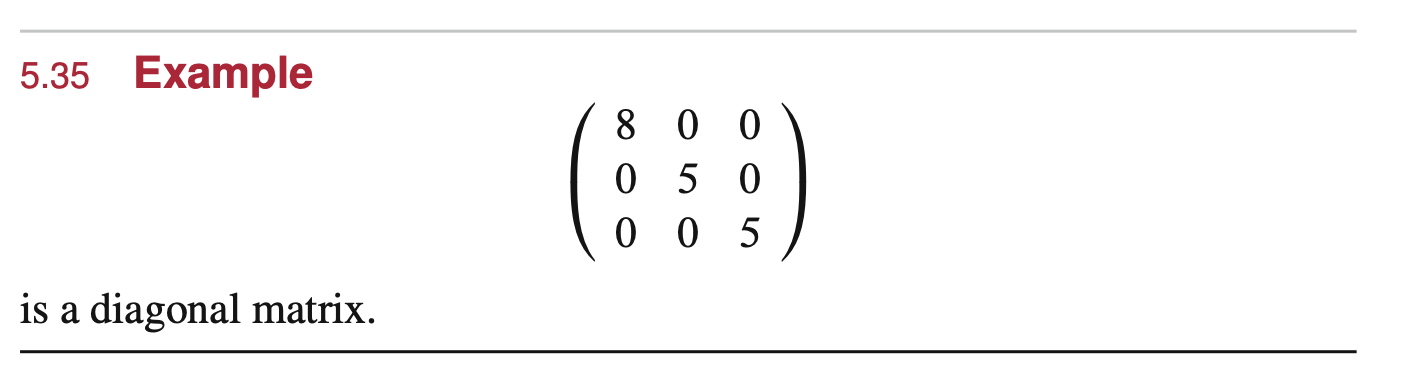
Furthermore, because eigenvalues of a map are the entries of the diagonal of its upper-triangular matrix, and this is technically an upper-triangular matrix, the entries on the diagonal are exactly the eigenvalues of the Linear Map.

properties of diagonal matrices

Suppose $V$ is finite-dimensional, and $T \in \mathcal{L}(V)$; and let $\lambda_{1}, … \lambda_{m}$ be distinct eigenvalues of $T$. Then, the following are equivalent:

$T$ is diagonalizable
$V$ has a basis containing of eigenvectors of $T$
there exists 1-dim subspaces $U_{1}, …, U_{n}$ of $V$, each invariant under $T$, such that $V = U_1 \oplus … \oplus U_{n}$
specifically, those $U$ are eigenspaces; that is: $V = E(\lambda_{1}, T) \oplus … \oplus E(\lambda_{m}, T)$
$\dim V = \dim E(\lambda_{1}, T) + … + \dim E(\lambda_{m}, T)$

Proof:

$1 \implies 2$, $2 \implies 1$

By a moment’s fucking thought. hehe my notes my rule. jkjkjk

By calculation this is true; if you apply a standard basis to the matrix, it will simply be scaled; therefore, you can think of each slot as an eigenvector of $T$.

$2 \implies 3$

Create $U_{j} = span(v_{j})$ where $v_{j}$ is the $j$ eigenvalue of $T$. Now, given $v_{j}$ forms a basis, then, $v_1 … v_{n}$ not only is linearly independent but span. Therefore, each vector in $V$ can be written uniquely by a linear combination of $v_{j}$ (i.e. taking one $v_{j}$ from each $U$). Hence, by definition, $U_{j}$ form a direct sum to $V$, hence showing $3$.

$3\implies 2$

Now, suppose you have a bunch of 1-d invariant subspaces $U_1 … U_{n}$ and they form a direct sum; because they are invariant subspaces, picking any $v_{j} \in U_{j}$ would be an eigenvector (because $T v_{j} = a_{j} v_{j}$, as applying $T$ is invariant so it’d return to the same space, just at a different place). Now, because they form a direct sum on $V$, taking $v_{j}$ from each $U_{j}$ would result in a linearly independent list which—because they sum up to $V$—span all of $V$ as each $U$ is simply spanning by scaling $v_{j}$. So, $v_{j}$ together forms a basis.

$2 \implies 4$

Given $V$ has a basis formed by eigenvectors of $T$, the sum of all scales of eigenvectors in $T$ can be written by the sum of all eigenspaces: that is $V = null(T-\lambda_{1} I) + … null(T- \lambda_{m} I)$ (recall that $E(\lambda_{j}, T) = null(T- \lambda_{j}I)$); as each eigenvalue for which the basis is formed can be found in each of these spaces, their sum would therefore equal to $V$ as this sum represents an linear combination of eigenvectors in $T$.

Now, sum of eigenspaces form a direct sum so we have that the sum is direct sum. Hence: $V = E(\lambda_{1}, T) \oplus … \oplus E(\lambda_{m}, T)$

$4 \implies 5$

$U_1 + \dots + U_{m}$ is a direct sum IFF $\dim (U_1 + \dots + U_{m}) = \dim U_1 + \dots + \dim U_{m}$ (see link for proof).

$5 \implies 2$

We are given that:

\begin{equation} \dim V = \dim E(\lambda_{1}, T) + \dots + \dim E(\lambda_{m}, T) \end{equation}

which means that taking a basis of each subspace provides a list of $\dim n$ long of eigenvectors. Now, each sub-list belonging to each space is linearly independent amongst themselves, and they will each be linearly independent against others as list of eigenvectors are linearly independent.

i.e.: if $a_1v_1 + … + a_{n} v_{n} = 0$, we can treat each chunk from each eigenspace as $u$, making $u_1 + … u_{m} = 0$; as they are eigenvectors from distinct eigenvalues, they are linearly independent so each will be $0$. Now, collapsing it into the basis of each eigenspace, this makes $a_{j}$ of the coefficients $0$ as well.

And all of this makes $v_1 … v_{n}$ a list of $\dim n$ long that is linearly independent; hence, it is a basis of $V$, as desired. $\blacksquare$

enough eigenvalues implies diagonalizability

If $T \in \mathcal{L}(V)$ has $\dim V$ distinct eigenvalues, then $T$ is diagonalizable.

Proof:

let $\dim V = n$. Pick eigenvectors $v_1 … v_{n}$ corresponding to distinct eigenvalues $\lambda_{1} … \lambda_{n}$. Now, eigenvectors coorsponding to distinct eigenvalues are linearly independent, and this is a list of $\dim n$ long that is linearly independent, so it is a basis of eigenvectors. Now, that means that the matrix coorsponding to $T$ is diagonalizable.

NOTE THAT THE CONVERSE IS NOT TRUE! as each eigenspace can have a dimension of more than 1 so 1 eigenvalue can generate two linearly independent eigenvectors belonging to it.

For instance:

\begin{equation} T (z_1, z_2, z_3) = (4z_1, 4z_2, 5z_3) \end{equation}