Direct Sampling is the act in probability to sample what you want from the distribution. This is often used when actual inference impossible. It involves. well. sampling from the distribution to compute a conditional probability that you want.
It basically involves invoking the Frequentist Definition of Probability without letting \(n \to \infty\), instead just sampling some \(n < \infty\) and dividing the event space by your sample space.
So, for instance, to compute inference on \(b^{1}\) given observations \(d^{1}c^{1}\), we can write:
\begin{equation} P(b^{1} | d^{1}, c^{1}) = \frac{P(b^{1}, d^{1}, c^{1})}{P(d^{1})P(c^{1})} \approx \frac{\sum_{i}^{} b^{i} = 1 \land d^{i} = i \land c^{i} = 1}{\sum_{i}^{} d^{i} =1 \land c^{i} = 1} \end{equation}
where \(a^{i}\) is the \(i\) th sample.
Direct Sampling a Baysian Network
We first obtain a topological sort of the system. For a graph with \(n\) nodes, we then obtain a list \(X_{1:n}\).
We can then obtain a Direct Sampling via simply sampling from this list. Whenever we need to sample some kind of conditional probability, we know that for every \(k_{i}\) we need to sample from, its parent conditions would have already been sampled because we are sampling in order of a topological sort so we can just sample the values from a subset of the conditioned set.
Likelihood Weighted Sampling
Likelihood Weighted Sampling is a change to the Direct Sampling approach which deals with the fact that Direct Sampling may oversample conditional probabilities as it is sampling sub-nodes an equal amount.
It is particularly useful when our priors are unlikely.
To do this, we first perform Direct Sampling as how you would normally. Now, say we get \(D=1\), \(C=1\), \(E=1\) for the Baysian Network presented below, the actual value we return would be whatever \(P(D|E) P(C|E)\).
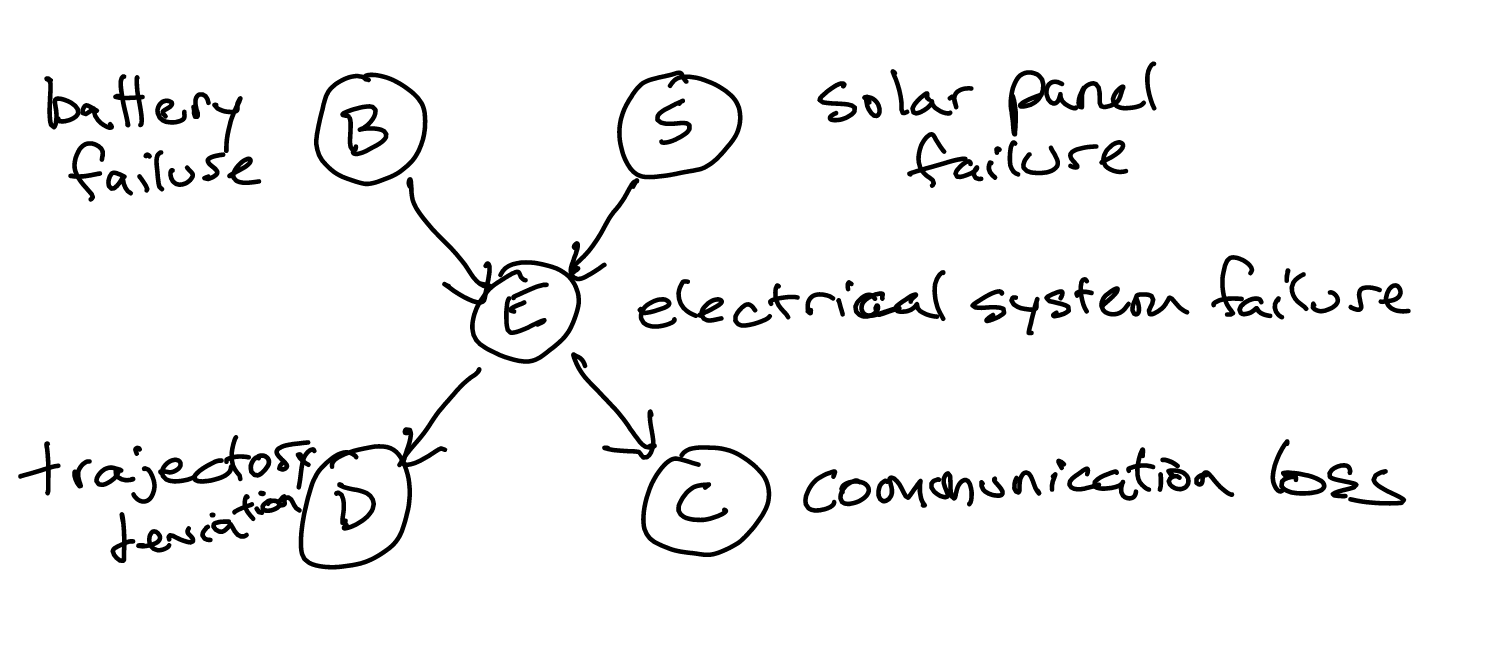
See an example here.