Though Coulomb’s Law allow us to calculate the force between any two individual charges, one can note that most of it is independent of the second test charge. In fact, each charge emits a field around itself of the shape:
\begin{equation} \vec{E( r)} = k \frac{q}{r^{2}} = \frac{1}{4\pi \epsilon_{0}} \frac{q}{r^{2}} \end{equation}
Or, you can think of it as moving a test charge \(q\) around the charge of interest, then calculating:
\begin{equation} \vec{E} = \frac{\vec{F_{e}}}{q} \end{equation}
As you can see, if the source charge were to be positive, you have a positive \(E\) which will point away from the charge, and negative charge \(E\) will point towards the charge.
One institution here that the above statement provides is that electric fields are drawn positive to negative; so, if you placed a positive test charge in the field, it will experience a force tangent to and in the same direction that traced out by the field lines. If you have a negative test change, then it will experience a force in the opposite direction.
additional information
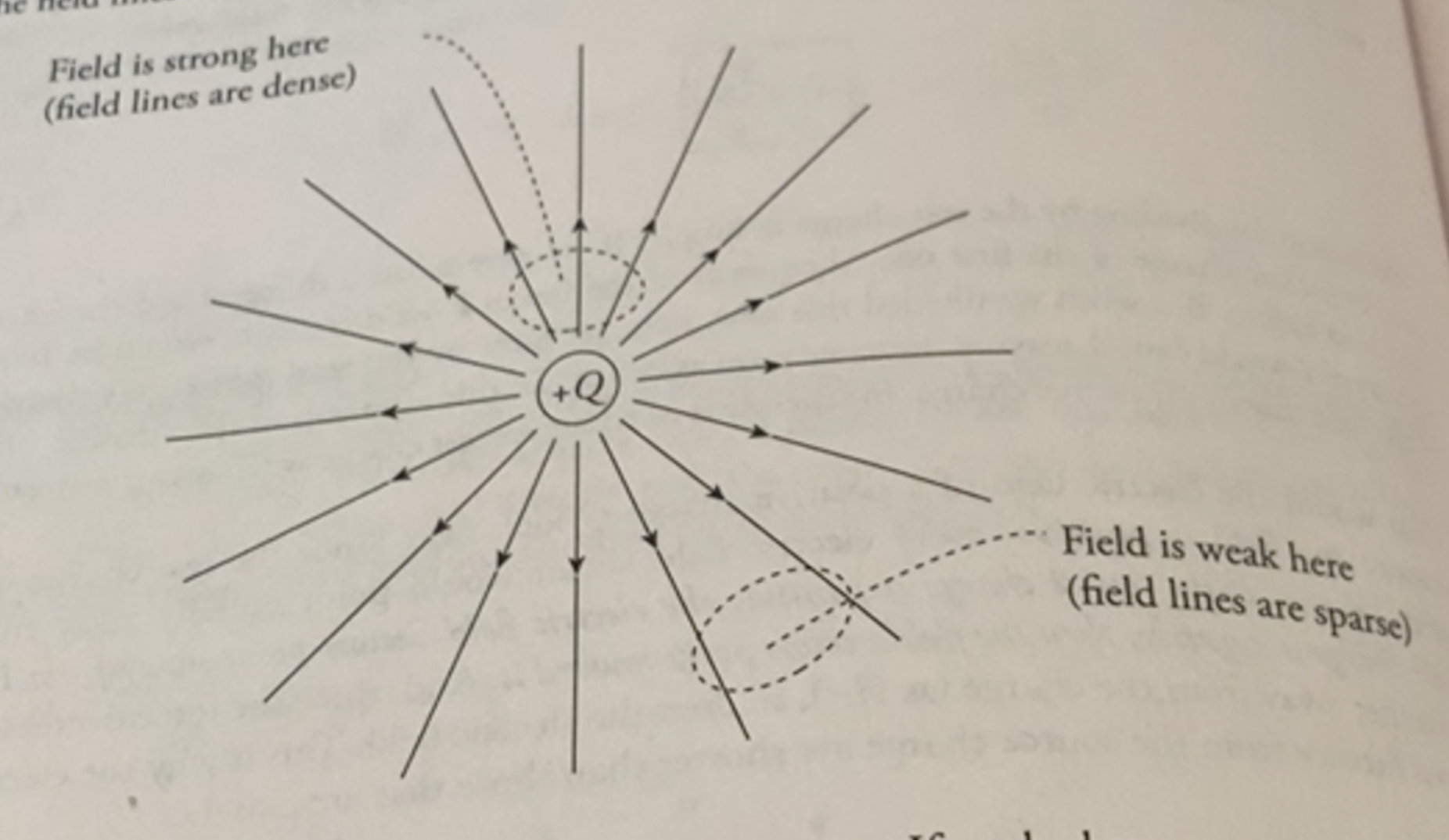
tracing electric field lines
By tracing out electric fields and observing the lines’ density, we can make a guess about how long the fields are.
composing electric fields
Unsurprisingly, superposition matters here as well:
If your system has multiple charges, then \(E_{total} = E_{q_1} + E_{q_2}\). No surprise here.