electric potential is analogous to gravitational potential energy, but with electrostatics!
\begin{equation} P_{E} = qV \end{equation}
where \(q\) is the change on the particle in question, and \(V\) is the voltage, the difference in electric potential between two places.
Yes, voltage is defined vis a vi electric potential: that is, it represents a differential of electric potential.
additional information
electric potential is analogous to gravitational potential
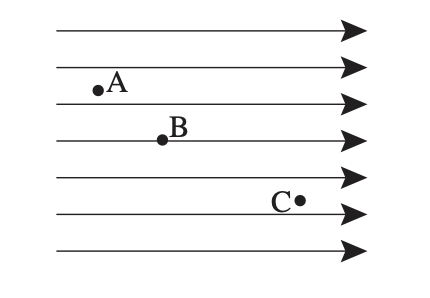
Let \(A, B, C\) be positrons, and the lines are the electric field. Which one has the highest electric potential? \(A\), because it has the most distance to travel to until it can get all the way to the right.
connecting electric potential and electric field
parallel plates
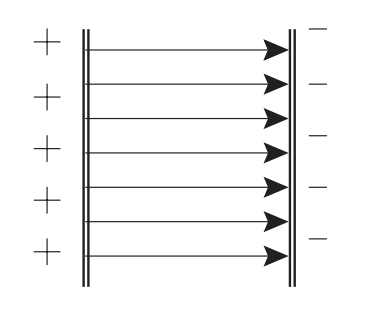
\begin{equation} E = \frac{V}{d} \end{equation}
where \(d\) is the distance between the plates, \(E\) the uniform electric field between the plates.
The amount of charge on each plate is described by:
\begin{equation} Q = CV \end{equation}
where, \(C\) is the capacitance of each plate, and \(V\) the voltage across the plates.