You are the president, and you are trying to choose the secretary of state. You can only interview people in sequence, and you have to hire on the spot. There are a known number of candidates. We want to maximize the probability of selecting the best candidate. You are given no priors.
How do we know which candidates we explore, and which candidates we exploit?
Sometimes, you don’t have a way of getting data.
Binary Bandit
We are playing with \(n\) binary slot machines.
- arm \(j\) pays off \(1\) with probability \(\theta_{j}\), and pays of \(0\) otherwise. we do not know $θj$s exogenously and have to learn it
- we only have \(h\) pulls in total across all \(n\) slot machines
As we perform \(k\) pulls, we can keep track of a separate Beta Distribution representing the probability of success for each of the slot machines.
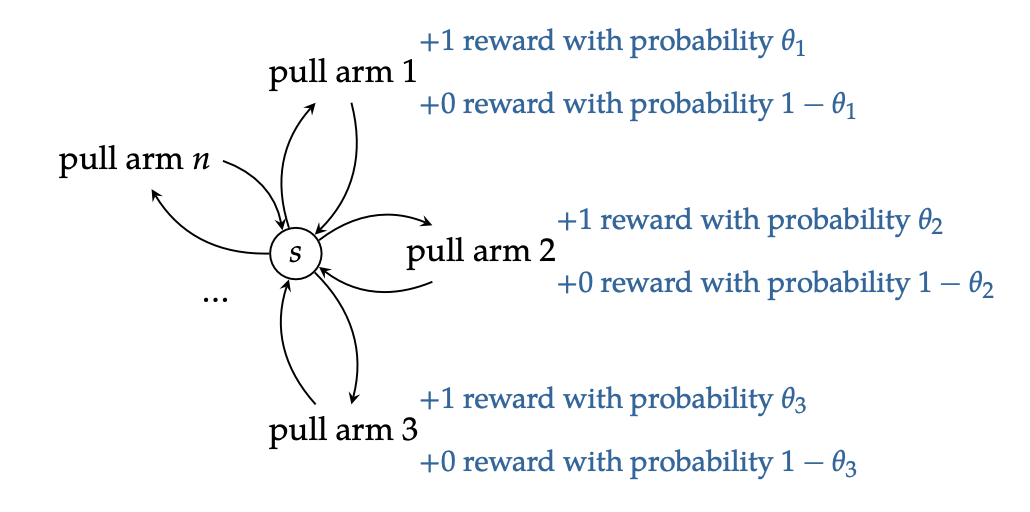
Essentially, we have a problem whereby we are at a stationary Markov Decision Process whereby the only difference between actions is how much reward we get.
Bayesian Model Estimation
We don’t actually know the probability of winning (called “\(\theta\)” in the figure above), and therefore have to “explore” the system to actually know about it.
We want to compute \(\rho_{a}\):
\begin{equation} \rho_{a} = P(win_{a} | w_{a}, l_{a}) = \int_{0}^{1} \theta \times Beta(\theta | w_{a}+1, l_{a}+1) \dd{\theta} \end{equation}
where, \(w_{a}\) is the number of successes for arm \(a\), and \(l_{a}\) is the number of failures observed.
This is exactly the \(\mathbb{E}[Beta(w_{a}+1, l_{a}+1)] = \frac{w_{a}+1}{(w_{a}+1)+(l_{a}+1)}\)
A “greedy action” is an action which simply chooses the \(a\) out of all \(\rho_{a}\) which maximizes this probability. We often don’t want that because we want to explore the space.
Approximate Exploration Strategies
Optimal Exploration
Optimal Exploration is not always possible because its computationally to complex. But its in theory possible. See Optimal Exploration.