The Gauss’ Law is a principle of electric flux of uniformly distributed electric field along a surface: that, the electric flux through a closed surface is the sum of the electric charge enclosed divided by the permittivity of free space.
That is:
\begin{equation} \oint E \cdot dA = \frac{\sum Q}{\epsilon_{0}} \end{equation}
somewhat motivating Gauss’ Law
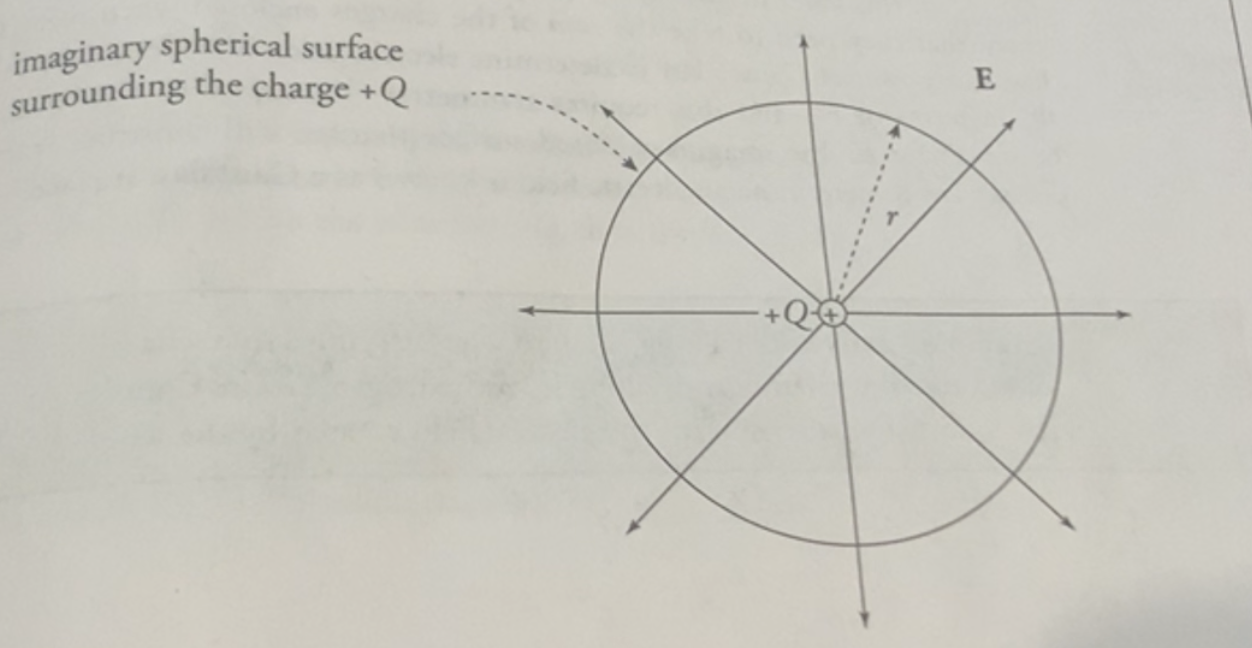
Consider a sphere with uniformly distributed charge on its surface. It has surface area \(4 \pi r^{2}\). Given the expression of electric flux and the fact that the origin change is in the center, and the test change is evenly distributed (i.e. \(E\) is held constant):
\begin{align} \Phi_{E} &= \int E \cdot dA \\ &= E\int dA \end{align}
Now, we are integrating across the entire surface of the sphere, so it is a closed integral. So:
\begin{align} \Phi_{E} &= \oint E dA \end{align}
We have the entire sum of the surfaces to be the surface area; so \(\oint dA = 4\pi r^{2}\). Furthermore, recall that if the field is uniform, \(E\) is constantly at \(\frac{1}{4 \pi \epsilon_{0}} \frac{Q}{r^{2}}\).
So, substituting the two in:
\begin{align} \Phi_{E} &= \frac{1}{4\pi \epsilon_{0}} \frac{Q}{r^{2}} 4\pi r^{2} \\ &= \frac{Q}{\epsilon_{0}} \end{align}
where, \(\epsilon_{0}\) is the permittivity of free space.
Congrats, we have Gauss’ Law: “the electric flux through the surface of an object is the sum of the charges enclosed divided by the permittivity of free space.”
spheres
electric field inside a closed conductor is zero
This is a direct result of gauss’ law