Belief iLQR

Motivation

Imperfect sensors in robot control: partial observations
Manipulators face tradeoff between sensing + acting

curse of dimensionality and curse of history.

Belief-Space Planning

Perhaps we should plan over all possible distributions of state space, making a belief-state MDP.

But: this is a nonlinear, stochastic dynamic. In fact: there maybe stochastic events that affects dynamics.

Big problem:

dim(belief) >> dim(state)
dim(belief) >> dim(action)

Belief iLQR

“determinize and replan”: simplify the dynamics at each step, plan, take action, and replan

tracks belief via observations
simplifies belief state dynamics based on linear MLE

When the dynamics is linear, you can use Linear-Quadratic Regulator to solve. This results in a worse policy but will give you a policy.

Previous Work

“just solve most-likely state”: doesn’t take action to explore and understand the state.
“belief roadmap”: not really planning in the belief space itself

Approach

Belief Update

We use Baysian updates for the state probably updates:

\begin{equation} P(s_{t+1}) = \eta P(o_{t+1}|s_{t+1}) \int_{x} p(_{t+1}|x, a_{t}) P(s) \end{equation}

and then the actual beliefs are updated with Extended Kalman Filter.

Importantly, the Extended Kalman Filter usually requires us to take an expectation of each observation O over all O; instead, we assume that the future states are uniform linearly distributed.

Belief Update Cost

Ideally, we want to lower covariance of the belief vectors in order to be more confident.

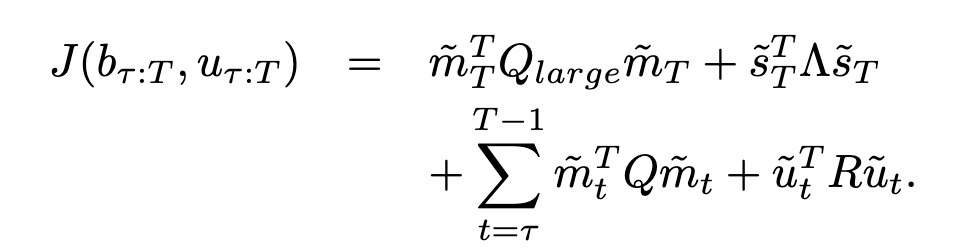
first term: reduce large trajectories (verify)
second: stabilization

Replanning Strategy

while b not at goal:
    # replan at where we are at now
    (b, a, mean_b) = create_initial_plan(b);

    for depth d:
        a_t = solve_lqr_for_plan_at_time(b, a, mean_b)
        o = environment.step(a_t)
        b = extended_kalman(b, a, o)

        if mean(b) > max_allowed_belief_uncertainty:
            break