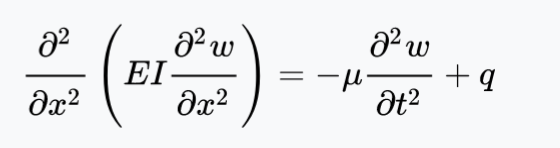Want mechanics? No. You get energy.
First, recall the stationary-action principle. To define a system in Lagrangian Mechanics, we define a smooth function \(L\), called the “Lagrangian”, and some configuration space (axis) \(M\).
By convention, \(L=T-V\). \(T\) is the kinetic energy in the system, and \(V\) is the potential energy in the system.
By the stationary-action principle, then, we require \(L\) to remain at a critical point (max, min, saddle.) This fact allows us to calculate the equations of motion by hold \(L\) at such a point, and evolving the \((T,V)\) pair to remain at that point.
The notion of solving for optimal \((T,V)\), which will give us the equations of motion, is why Lagrangian multipliers were invented.
Now, here’s a few results which help you deal with the Lagrangian.
Conservation of Momentum
Note that momentum is always conserved.
Recall that:
\begin{equation} F = m a = m \dv{v}{t} = \dv{mv}{t} \end{equation}
when \(m\) is constant, which it almost certainly is.
Recall the definition of momentum:
\begin{equation} p := mv \end{equation}
Therefore, we have that:
\begin{equation} F = \dv{p}{t} \end{equation}
Great, now let’s recall what energy is:
\begin{equation} W = \int F\dd{x} \end{equation}
Substituting our definitions of force:
\begin{equation} W = \int \dv{p}{t}\dd{x} = \int \dd{p}\dv{x}{t} = \int v \dd{p} \end{equation}
[something something something ask leonard]
We end up with:
\begin{equation} \pdv{W}{v} = p \end{equation}
how? IDK. But you then usually would use this by taking the derivative of the Lagrangian by velocity, then figuring it lingual to \(0\).
Beam Theory
We begin with this Euler-Lagrange expression:
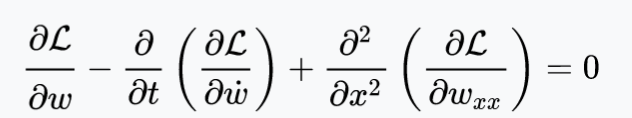
these are a series of expressions derived to semiautomatically solve Largrangian expressions of expressions derived to semiautomatically solve Largrangian expressions: they are the pre-figured-out stationary-action principle “stationary points” with the least energy.
We want to create a Lagrangian of our system, and plug it in there.
We define the Lagrangian for this system to be
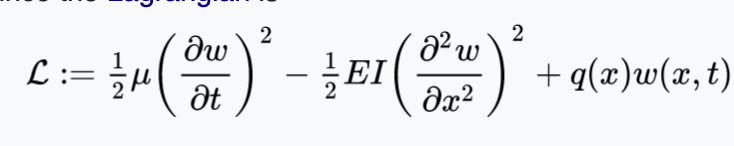
Recall that the Lagrangian is defined by all kinetic energy sum minus all potential energy sum. Will investigate deeper later, but the first term is obviously the kinetic energy (1/2 mass-density velocity squared), then the subtracted potential energy term is the spring potential of the system (1/2 kx^2).
Then there’s this third term. No idea.
We then try to plug stuff into that Euler-Lagrange expression. We can calculate for ourselves that:
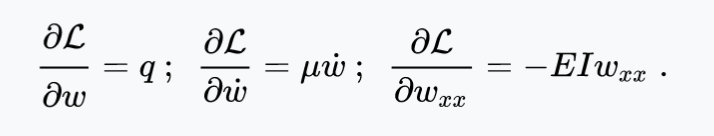
Finally, then:
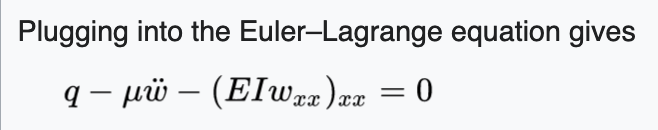
literally… the end. We just move stuff around and that’s literally it.