Autonomously driving is really hard. How do we integrate planning + learning in a close-loop style. We’ll start from the current belief, and construct a tree of all reachable belief state.
Recall DESPOT.
Approach
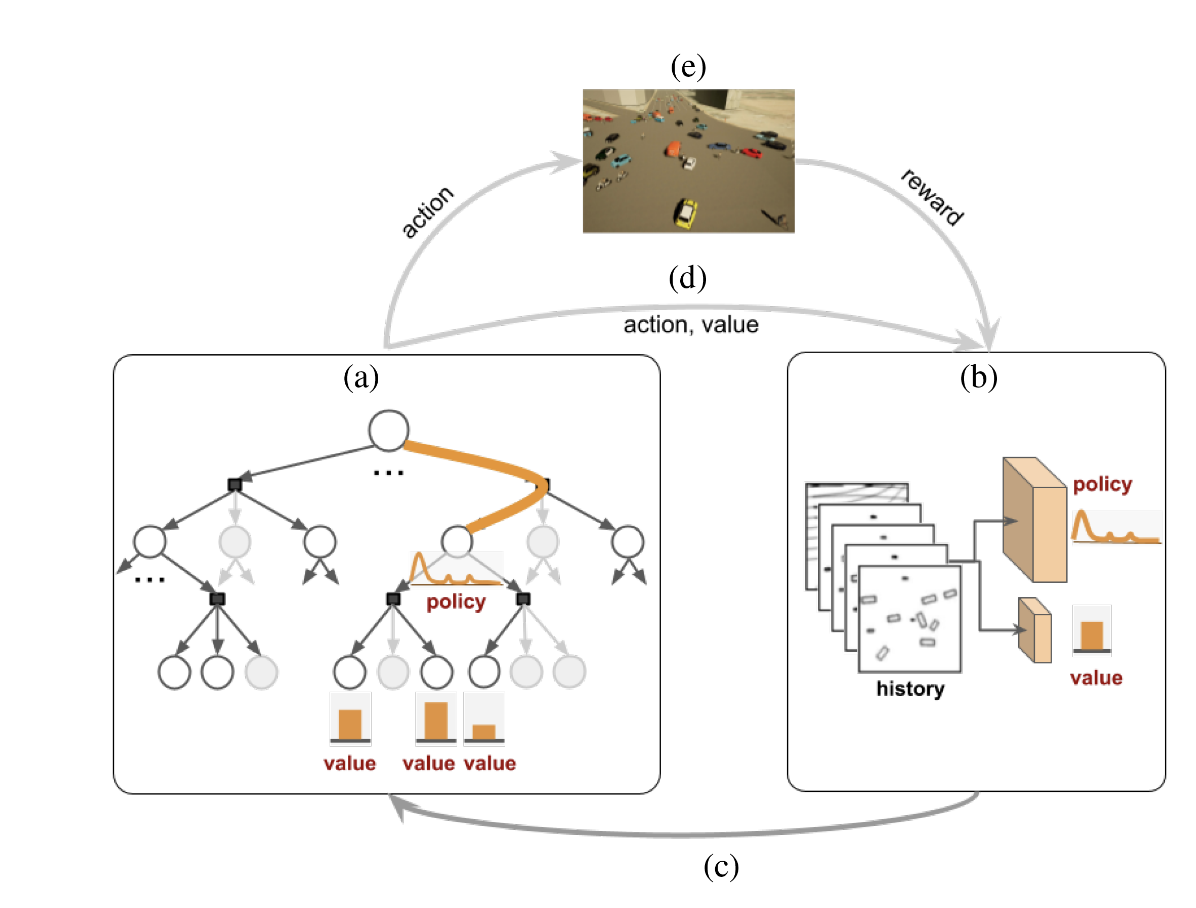
- learning (b): a neural network which maps the driving history into a policy and value
- planning (a): we will use the neural network’s derived policy and value to run MCTS
- execution (e): execute the actions in a simulator
The data which is obtained using the simulator is used to train the neural network.
learning
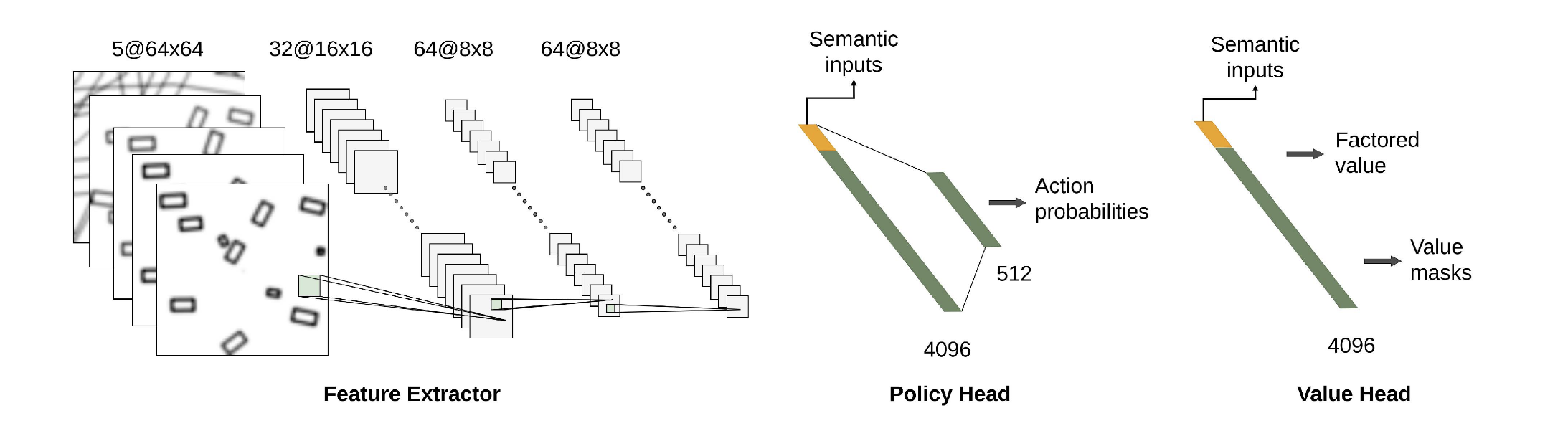
The learning component is a supervised policy where a CNN takes a situation and map
planning
its a AR-DESPOT. We select actions by:
\begin{equation} a^{*} = \arg\max_{a \in A} \left\{u(b,a) + c \pi_{\theta}(a|x_{b}) \sqrt{ \frac{N(b)}{N(b,a)+1}}\right\} \end{equation}
where \(\pi_{\theta}\) is our policy network.
Every time we encounter a new node, use the learned value function as a lower bound.
Needed less depth in the DESPOT than using it naively.