Gaussian Elimination Quiz
- Demonstrate that matrices’ multiplication are not commutative (error: didn’t consider \(m\times m\))
- Which \(2\times 2\) matrices under multiplication form a group? (error: closure need to proved on invertable matrices under multiplication, not just \(2\times 2\))
- Deriving Rotation matrices (error: clockwise vs counter-clockwise)
Linear Independence Quiz
- Connection between linear independence and systems equations (error: beated around the bush) — the matrix of an nxn system of equations has a solution if the matrix’s column vectors is linearly independent
Basis and Dimension Quiz
- put 0 into a basis AAAA not lin. indep; figure out what the basis for a polynomial with a certain root is: it is probably of dimension m (instead of m+1), because scalars doesn’t work in the case of p(3)=0; so basis is just the scalars
- missing some inequality about basis? — its just that lin.idp sets is shorter or equal to basis and spanning sets is longer or equal to basis
Final, part 1
- definition of vector space: scalar multiplication is not an operation
- straight forgot \(dim(U+V) = dim U + dim V - dim (U\cap V)\)
- plane containing \((1,0,2)\) and \((3,-1,1)\): math mistake
- proof: det A det B = det AB
Final, part 2
- Counterproof: If \(v_1 \dots v_4\) is a basis of \(V\), and \(U\) is a subspace of \(V\) with \(v_1, v_2 \in U\) and \(v_3, v_4\) not in \(U\), \(v_1, v_2\) is a basis of \(U\)
- Counterproof: if \(T \in \mathcal{L}(V,V)\) and \(T^{2}=0\), then \(T=0\)
- Counterproof: if \(s,t \in \mathcal{L}(V,V)\), and \(ST=0\), then \(null\ s\) is contained in \(range\ T\)
Product Spaces Quiz
Prove that \(\mathcal{L}(V_1 \times V_2 \times \dots \times V_{m}, W)\) and \(\mathcal{L}(V_1, W) \times \dots \times \mathcal{L}(V_{m}, W)\) are isomorphic
error: didn’t do it
Quotient Spaces Quiz
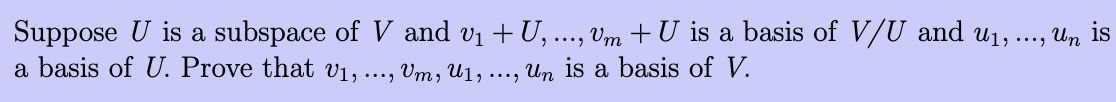
- Couldn’t prove that the list in linearly independent: the linear combinations is some \(c_1v_1 + \dots c_{m}v_{m} + U\); as \(v_1 \dots v_{m}\) is a basis of \(V / U\), \(c_1 \dots c_{m} = 0\), now the second part is also a basis so they are \(0\) too.
- The spanning proof: \(v + U =\) , rewrite as basis, etc.