For a charge to do something in a magnetic field, it has to have velocity; nothing happens without movement.
So:
\begin{equation} \vec{F}_{M} = q \vec{v} \times \vec{B} \end{equation}
To calculate: magnitude: \(qvB \sin \theta\) + right hand rule.
Radius
You maybe asked to find the radius of the path the particle takes, so:
\begin{equation} \frac{v^{2}}{r} = a \end{equation}
So, the net force here is:
\begin{equation} qvB = Ma \end{equation}
So plug in and solve
Current along a wire
\begin{equation} \vec{F} = \int I \dd{l} \times \vec{B} \end{equation}
The sum of the current across the wire is the same as \(q \vec{v}\).
This equals \(IlB \sin \theta\) in magnitude for constant current.
“FILB - sintheta”
Induced magnetic field
For the induced magnetic field of a current, use the curvey (curl) right hand rule.
The actual magnitude induced by the wire is ampere’s law:
\begin{equation} \oint \vec{B} \cdot \dd{\vec{l}} = \mu I \end{equation}
where, \(u_0\) is vacuum permeability (\(4 \pi \times 10^{-7} \frac{T \cdot m}{A}\)).
Magnetic Field of a Solenoid
\begin{equation} Bs = \mu_{0} n I \end{equation}
where, \(n = \frac{N}{L}\), the number of turns of the solenoid per length.
Magnetic Field of a Loop
\begin{equation} B 2\pi r = \mu_{0} I \end{equation}
where, the surface integral of length of a loop is just the circumference
WIRES ARE OPPOSITE
Current’s induced magnetic fields in the same direction attracts, and in opposite directinos repel
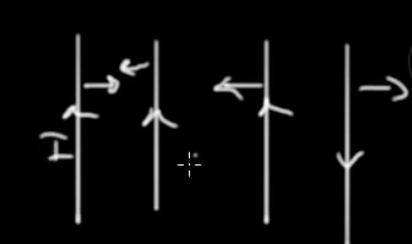
Full description of magnetic field non-bdl-b
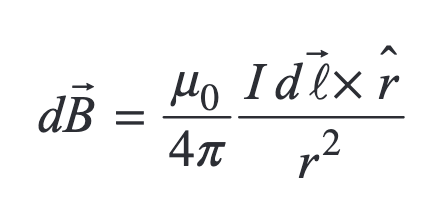
For instance, current in a loop and desire magnetic field in the center