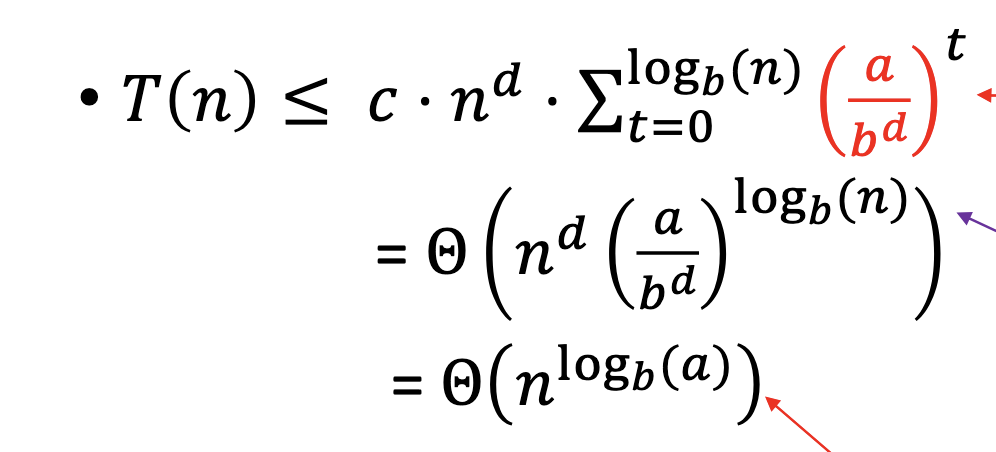A general recurrence relation solution formula. It’s a generalization of the “tree” method in example 1.
intuition
Every Recursion Theorem problem has a struggle between most work sitting at the “bottom” of the tree (number of subproblems explode, \(a > b^{d}\)) vs most work sitting at the “top” of the tree (problem lower in the tree are smaller, \(a < b^{d}\)).
constituents
Consider:
- \(a\): number of subproblems
- \(b\): input size shrink
- \(d\) need to do \(n^{d}\) work to merge subproblems
Suppose \(a \geq 1, b> 1\), and \(d\) are constants. Suppose \(T\qty(n) = aT\qty(\frac{n}{b}) + O\qty(n^{d})\), we then have:
requirements
\begin{equation} T\qty(n) = \begin{cases} O\qty(n^{d}\log\qty(n)), \text{ if } a = b^{d}\\ O\qty(n^{d}), \text{ if } a < b^{d}\\ O\qty(n^{\log_{b} \qty(a)}), \text{ if } a > b^{d}\\ \end{cases} \end{equation}
additional information
proof
Suppose that \(T\qty(n) \leq a\cdot T\qty(\frac{n}{b}) + c \cdot n^{d}\). We desire the master theorem’s statement. Consider a standard tree argument via merge sort. At each layer, the input size gets cut by \(b\), so we obtain \(\log_{b} \qty(n)\) layers of the tree.
Filling things out we get the following table:
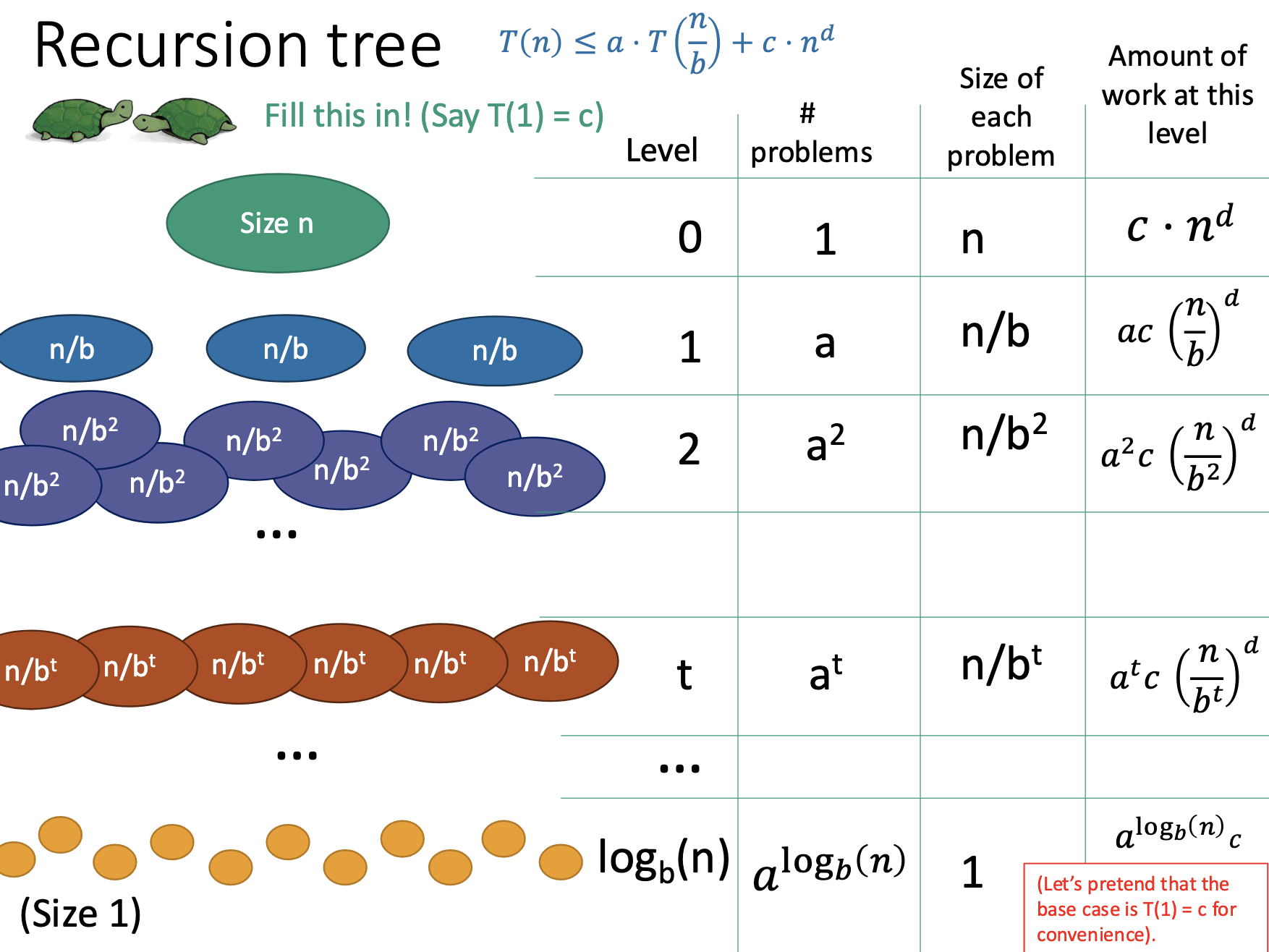
Adding up the work of this table:
\begin{align} \sum_{t=0}^{\log_{b}n} a^{t} c \qty(\frac{n}{b^{t}})^{d} &= cn^{d}\sum_{t=0}^{\log_{b}n} a^{t}\qty(\frac{1}{b^{t}})^{d} \\ &= cn^{d}\sum_{t=0}^{\log_{b}\qty(n)} \qty(\frac{a}{b^{d}})^{t} \end{align}
The master theorem therefore splits equation into three components based on the ratio \(\frac{a}{b^{d}}\):
\(a = b^{d}\)
So we obtain:
\begin{align} c n^{d} \sum_{t=0}^{\log _{b}\qty(n)} 1 = c n^{d} \qty(\log_{b}\qty(n)+1) = \theta\qty(n^{d}\log\qty(n)) \end{align}
\(a < b^{d}\)
Recall bounded geometric sum. Notice that if \(a < b^{t}\), then \(\qty(\frac{a}{b^{d}})^{t}\) should be \(x^{t}, x< 1\), so its bounded by a constant.
Hence:
\begin{align} c n^{d} \sum_{t=0}^{\log _{b}\qty(n)} \qty(\frac{a}{b^{d}})^{t} = cn^{d}\theta\qty(1) = \theta \qty(n^{d}) \end{align}
\(a > b^{d}\)