maximum a posteriori estimate is a parameter learning scheme that uses Beta Distribution and Baysian inference to get a distribution of the posterior of the parameter, and return the argmax (i.e. the mode) of the MAP.
Calculating a MAP posterior, in general:
\begin{equation} \theta_{MAP} = \arg\max_{\theta} P(\theta|x_1, \dots, x_{n}) = \arg\max_{\theta} \frac{f(x_1, \dots, x_{n} | \theta) g(\theta)}{h(x_1, \dots, x_{n})} \end{equation}
We assume that the data points are IID, and the fact that the bottom of this is constant, we have:
\begin{equation} \theta_{MAP} = \arg\max_{\theta} g(\theta) \prod_{i=1}^{n} f(x_{i}|\theta) \end{equation}
Usually, we’d like to argmax the log:
\begin{equation} \theta_{MAP} = \arg\max_{\theta} \qty(\log (g(\theta)) + \sum_{i=1}^{n} \log(f(x_{i}|\theta)) ) \end{equation}
where, \(g\) is the probability density of \(\theta\) happening given the prior belief, and \(f\) is the likelyhood of \(x_{i}\) given parameter \(\theta\).
You will note this is just Maximum Likelihood Parameter Learning function, plus the log-probability of the parameter prior.
MAP for Bernoulli and Binomial \(p\)
To estimate \(p\), we use the Beta Distribution:
The MODE of the beta, which is the MAP of such a result:
\begin{equation} \frac{\alpha -1 }{\alpha + \beta -2} \end{equation}
now, for a Laplace posterior \(Beta(2,2)\), we have:
\begin{equation} \frac{n+1}{m+n+2} \end{equation}
MAP for Poisson and Exponential \(\lambda\)
We use the gamma distribution as our prior
\begin{equation} \Lambda \sim Gamma(\alpha, \beta) \end{equation}
where \(\alpha-1\) is the prior event count, and \(\beta\) is the prior time periods.
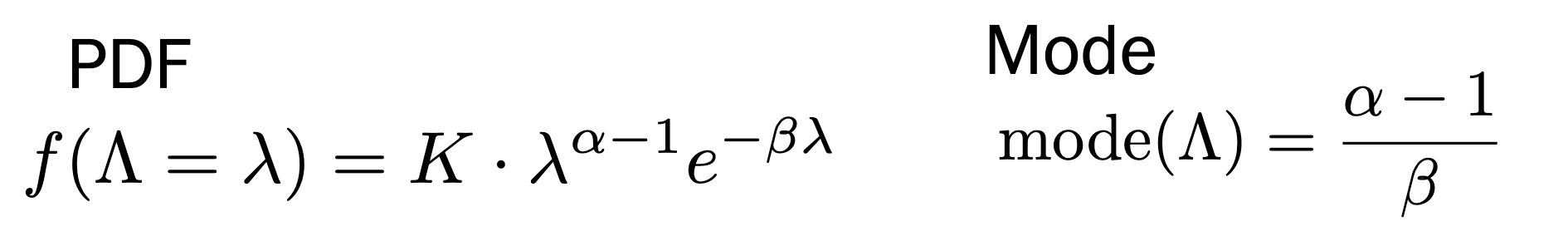
Let’s say you have some data points \(x_1, …x_{k}\), the posterior from from those resulting events:
\begin{equation} Gamma(\alpha + n, \beta+k) \end{equation}