“We find the parameter that maximizes the likelihood.”
- for each \(X_{j}\), sum
- what’s the log-likelihood of one \(X_{i}\)
- take derivative w.r.t. \(\theta\) and set to \(0\)
- solve for \(\theta\)
(this maximizes the log-likelihood of the data!)
that is:
\begin{equation} \theta_{MLE} = \arg\max_{\theta} P(x_1, \dots, x_{n}|\theta) = \arg\max_{\theta} \qty(\sum_{i=1}^{n} \log(f(x_{i}|\theta)) ) \end{equation}
If your \(\theta\) is a vector of more than \(1\) thing, take the gradient (i.e. partial derivative against each of your variables) of the thing and solve the place where the gradient is identically \(0\) (each slot is \(0\)). That is, we want:
\begin{equation} \mqty[\pdv{LL(\theta)}{\theta_{1}} \\ \pdv{LL(\theta)}{\theta_{2}} \\ \pdv{LL(\theta)}{\theta_{3}} \\ \dots] = \mqty[0 \\ 0 \\0] \end{equation}
MLE is REALLY bad at generalizing to unseen data. Hence why MLE is good for big data where your MLE slowly converge to best parameters for your actual dataset.
We desire \(\theta\) parameter from some data \(D\). To do this, we simply optimize:
\begin{equation} \hat{\theta} = \arg\max_{\theta}P(D|\theta) \end{equation}
, where:
\begin{equation} P(D|\theta) = \prod_{i} P(o_{i}| \theta) \end{equation}
for each \(o_{i} \in D\). and \(P\) is the likelyhood: PMF or PDF given what you are working with.
That is, we want the parameter \(\theta\) which maximizes the likelyhood of the data. This only works, of course, if each \(o_{i} \in D\) is independent from each other, which we can assume so by calling the samples from data IID (because they are independent draws from the underlying distribution.)
log-likelihood
The summation above is a little unwieldy, so we take the logs and apply log laws to turn the multiplication into a summation:
\begin{equation} \hat{\theta} = \arg\max_{\theta} \sum_{i} \log P(o_{i}|\theta) \end{equation}
“add the log probabilities of each of the outcomes you observed happening according to your unoptimized theta, and maximize it”
argmax of log
This holds because log is monotonic (“any larger input to a log will lead to a larger value”):
\begin{equation} \arg\max_{x} f(x) = \arg\max_{x} \log f(x) \end{equation}
MLE, in general
\begin{equation} \theta_{MLE} = \arg\max_{\theta} \qty(\sum_{i=1}^{n} \log(f(x_{i}|\theta)) ) \end{equation}
Example
Say we want to train a model to predict whether or not a plane will crash. Suppose our network is very simple:
\(\theta\) represents if there will be an midair collision. Therefore, we have two disconnected nodes:
\begin{equation} P(crash) = \theta \end{equation}
\begin{equation} P(safe) = 1-\theta \end{equation}
Now, suppose we observed that there was \(m\) flights and \(n\) midair collisions between them. We can then write then:
\begin{equation} P(D|\theta) = \theta^{n}(1-\theta)^{m-n} \end{equation}
because \(\theta^{n}(1-\theta)^{m-n}\) is the total probability of the data you are given occurring (\(n\) crashes, \(m-n\) non crashing flights).
Now, we seek to maximise this value—because the probability of \(P(D)\) occurring should be \(1\) because \(D\) actually occured.
Its mostly algebra at this point:
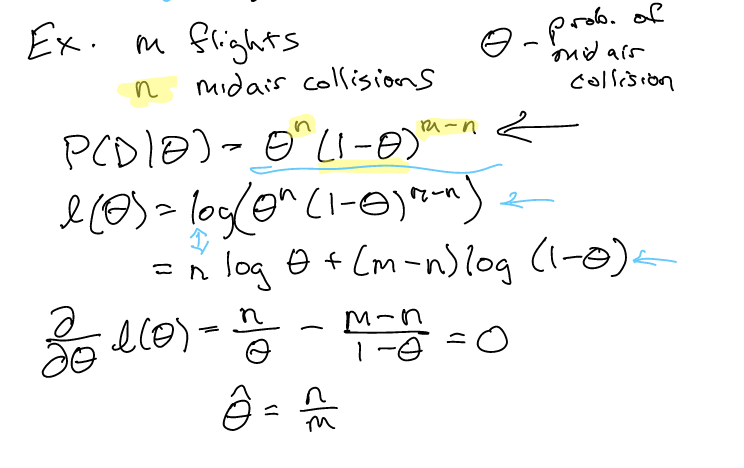
Steps:
- we first compute the probability of each of the sample happening according to old \(\theta\) to get \(P(D|\theta)\)
- we then take the log of it to make it a summation
- we then try to maximize \(\theta\) to
What this tells us is…
Generic Maximum Likelihood Estimate
Overall, its kind of unsurprising from the Frequentist Definition of Probability, but:
\begin{equation} \hat{\theta}_{i} = \frac{n_{i}}{\sum_{j=1}^{k} n_{j}} \end{equation}
for some observations \(n_{1:k}\).
and:
\begin{equation} \sigma^{2} = \frac{\sum_{}^{} (o_{i} - \hat{u})^{2}}{m} \end{equation}
Problems with Maximum Likelihood Parameter Learning
This requires a lot of data to make work: for instance—if we don’t have any plane crashes observed in \(n\) files, this scheme would say there’s no chance of plane crashes. This is not explicitly true.
Therefore, we use Baysian Parameter Learning.