Minimizing DFAs

The fact that DFAs are limited, it allows us to optimize a DFA. Specifically, we ask: “does this DFA have a minimal number of states?”

Formally: can we accept the same language with a particular DFA with another DFA with less states?

For every language $L$, there is a unique (up to state relabeling) minimal-state DFA $M^{*}$ such that $L(M^{*}) = L$.

Furthermore, there exists an efficient algorithm which, given DFA $M$, will produce this unique $M^{*}$.

(btw; there isn’t a uniquely minimal NFA)

Now let’s show it; in many parts.

extending $\delta$

Given a DFA, we want to extend its transition function to $\Delta: Q \times \Sigma \to Q$ (i.e. string transitions instead of character transitions)

\begin{align} &\Delta (q, \varepsilon) = q \\ &\Delta (q, \sigma) = \delta(q, \sigma) \\ &\Delta (q, \sigma_{1} \dots \sigma_{k+1}) = \delta(\Delta(q, \sigma_{1} \dots\sigma_{k}), \sigma_{k+1}) \end{align}

Meaning, $\Delta(q,w)$ is the state $M$ reached after reading $w$, starting from state $q$. Meaning, $\Delta(q_0, w) \in F$ means IFF that $w \in L(M)$.

So: $w \in \Sigma^{*}$ distinguishes states $q_1, q_2$ if $Δ(q_1, w) ∈ F ⇔ Δ(q_2, w) ¬ ∈ F$—this is because if the right is true, passing $w$ at each of those states do not allow you to forget where you started with (as transitions of both after $q_1$ and $q_2$ are the same). Hence, those states are distinguished by $w$. That is, $w$ allows you to tell which one of $q_1$ or $q_2$ you are in.

distinguishable states

We define state $p$ as distinguishable from state $q$ if there exists some $w \in \Sigma^{*}$ such that exactly one of $\Delta(p,w)$ or $\Delta(q,w)$ is an accept state. That is, $w$ distinguishes $p$ and $q$.

This means that these two states have a different function: you can’t merge them.

Conversely, state $p$ and $q$ are indistinguishable if they are not distinguishable; that is, for all $w \in \Sigma^{*}$, $\Delta(p,w) \in F \Leftrightarrow \Delta(q,w) \in F$.

Indistinguishable states are redundant.

~

Let us define a binary relation ~ on the states of $M$. Specifically, $p \sim q$ IFF $p$ is indistinguishable from $q$. That is, $p \not\sim q$ if $p$ is distinguishable from $q$.

$\sim$ is an equivalence relation.

state partitioning

since ~ is an equivalence relation, we can partition states $Q$ into disjoint equivalence classes.

that is, each of the equivalence relation for $q$ means that $[q] := \qty {p | p \sim q}$; because of transitivity, naming any element of this group will give you the whole group.

DFA minimization algorithm

input: DFA $M$
output: DFA $M_{\min}$ such that…
- $L(M) = L\qty(M_{MIN})$
- $M_{MIN}$ has no inaccessible states (remove any states not accessible from the start state)
- $M_{MIN}$ is irreducible: for all states $p,q\neq p \in Q_{M_{MIN}}$, $p \not \sim q$

steps

remove inaccessible states

lol

table-filling algorithm

we now want to obtain all of our non distinguishable equivalent state classes.

Scratch-work:

States of $M_{MIN}$ will be the equivalence classes of the states of $M$; we cover these equivalence classes with a DP algorithm.

Build a DP table: $D_{M} =\qty {(p,q) | p,q \in Q, p \sim q}$.
Cluster them into equivalence classes: $EQUIV_{M} = \qty {[q] | q \in Q}$

To build this table: we know how to find the pairs that $\varepsilon$ distinguishes; then, we iterate to lengthen string length and find those pairs distinguishable with longer strings. The pairs of states then left over would be indistinguishable.

base case: $(p,q)$ such that $p$ accepts and $q$ rejects, because they are distinguished by the empty string.
iteration: for each grid $p,q$ and see if any symbol $\sigma \in \Sigma$ satisfy—for $\delta (p, \sigma) = p’$, $\delta (q, \sigma) = q’$, we have $p’ \not \sim q’$; if that’s the case, then $p \not \sim q$
we repeat until no more slots can be marked as non-distinguishable by going through an entire iteration without change

Time complexity: $O(|\Sigma| |q|^{2})$ (we go through each vocab item for each state). This algorithm iterates for at most $q^{2}$ times.

theorem: $M_{MIN}$ is the unique minimal DFA that is equivalent to $M$.

define our new DFA

\begin{equation} M_{MIN} = \qty(Q_{MIN}, \Sigma, \delta_{MIN}, q_0_{MIN}, F_{MIN}) \end{equation}

we will define these vis a vi our new equivalence classes:

\begin{equation} Q_{MIN} = EQU_{M}, q_{0}_{MIN} = \qty[q_0], F_{MIN} = \qty {[q] | q \in F} \end{equation}

the transition function just needs to apply that of m on one member of your equivalence class:

\begin{equation} \delta_{\min}\qty([q], \sigma) = \qty[\delta(q, \sigma)] \end{equation}

this accepts the same language due to the definition of indistinguishable states (i.e. these equivalence classes).

properties

as a by product, this algorithm bounds the shortest distinguishing string between two distinguishable states by $q^{2}$ because at each iteration of the algorithm it add at most one char to the end of the distinguishing string, and our system runs at most $q^{2}$ times

proof that table-filling algorithm works

if $(p,q)$ is marked, then $p \not\sim q$.

Proof:

We do induction. Invariant: whatever happened before is correct.

Base case: if $(p,q)$ is marked $D$ at the start, then one state is in $F$ and the other isn’t, and so $\varepsilon$ distinguishes $p$ distinguishes $q$.

Suppose $(p,q)$ is marked $D$ at a later point, then there exists states $p’, q’$ such that $p’ \not \sim q’$ and also $p’ = \delta (p, \sigma )$ and $q’ = \delta (q, \sigma)$.

Given $p’ \not \sim q’$, there’s a string $w$ such that $\Delta(p’, w) \in F \Leftrightarrow \Delta (q’, w) \not \in F$; since we know there exists a symbol $\sigma$ to get from $p,q$ to $p, q$, we can concatenate that to $w$ like so ($\sigma w$, processing our new symbol before the rest of the string) to show that $\Delta(p, w) \in F \Leftrightarrow \Delta (q, w) \not \in F$, so $p \not \sim q$.

if $(p,q)$ is not marked, then $p \sim q$.

Let’s prove this by contradiction.

Suppose for contradiction the pair $(p,q)$ is not by $D$, yet $p \not \sim q$. Since $p \not \sim q$, then there exists a string $w$ such that $|w| > 0$ (this is true because if $w$ was the empty string it would fall into our base case already), $\Delta(p, w) \in F \Leftrightarrow \Delta (q, w) \not \in F$.

If there are many such bad pairs, we choose the one with the shortest distinguishing string $w$ that marks them.

Since $w’$ is non-empty, let’s write $w = \sigma w’$. Let $p’ = \delta (p, \sigma)$ and $q’ = \delta(q, \sigma)$.

So, this means that $p’ \not \sim q’$ (because we just play the rest of $w’$ to distinguish them)—yet, they wouldn’t have been marked because if they did our algorithm would have then marked $p \not \sim q$ as well. This means that also $p’$ and $q’$ is also a bad pair.

Yet, we chose $p, q$ to be the bad pair with the shortest distinguishing string; $p’, q’$ have shorter distinguishing strings (namely, $w’$). So, we reach contradiction.

DFA minimization is unique

theorem: $M_{MIN}$ is the unique minimal DFA that is equivalent to $M$.

theorem proof

if $M’$ is a another minimal DFA for $M$, then $M’$ has no inaccessible states and is irreducable; then, lemma 1 applies so there is an isomorphism between $M’$ and $M_{MIN}$.

lemma 1

Lem. 1: Suppose there’s some irreducible $M’$ where $L(M’) = L(M_{\min})$ with no inaccessible states; we have that there exist an isomorphism between $M’$ and $M_{\min}$.

Proof:

we need to construct such an isomorphism.

$q_0_{\min} \to q_0’$
recursion:
- if $p_{\min} \to p’$ and $\delta_{\min}(p_{\min}, \sigma) =q_{\min }$ and $\delta’(p’, \sigma) =q’$
- then we assign $q_{\min } \to q’$

to show isomorphism

defined everywhere
well defined
bijective
preserve all transitions (for all $p \to p’$, then $\delta_{\min}(p, \sigma) \to \delta’(p’, \sigma)$

defined everywhere

for all states $q$ of $M_{\min }$, there exists $q’$ of $m’$ such that $q \to q’$

if $q \in M_{\min}$, then there is a string $w$ such that $\Delta_{\min}(q_0_{\min}, w) = q$. let $q’ = \Delta’(q’_{0}, w)$, then $q \to q’$.

we show this by inducing the fact that we can define the mapping of these stages one at a time.

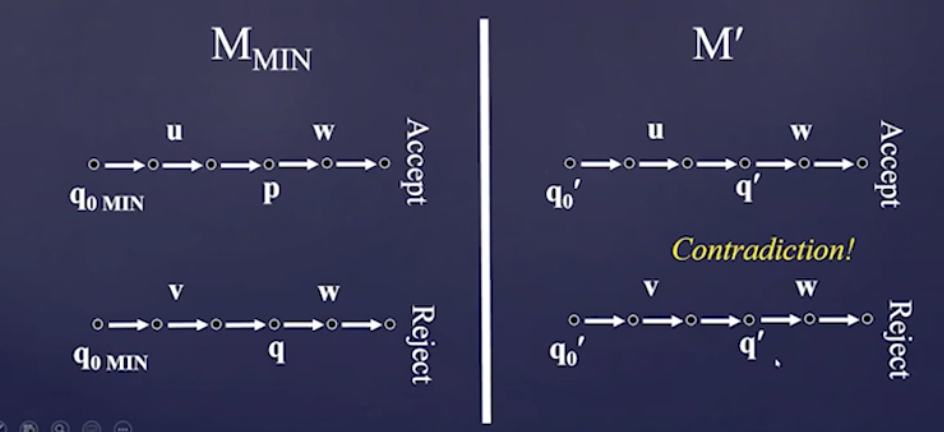
one-to-one (injective)

we show this as a contradiction.

suppose by contradiction $p \neq q$ such that $p \to q’$ and $q \to q’$; again, this means that we would (like in the well-defined case, but this time in $M_{\min }$ now), tack on a string which sends us to accept and reject cases

surjective

for all states $q’$ of $M’$, there exists a state $q$ of $M_{\min}$ such that $q \to q’$.

we can show this by noticing that for every state $q’$ in $M’$, we have some string $w$ which $M’$ reaches to get there. we define $q$ as the state of $M_{\min}$ after applying $w$. We claim $q \to q’$.

well-defined

this needs to be a function, so we can’t have cases where its $q \to q’$ yet also $q \to q’’$ where $q’ \neq q’’$.

suppose for contradiction $q’$ and $q’’$ are distinguishable in $M$

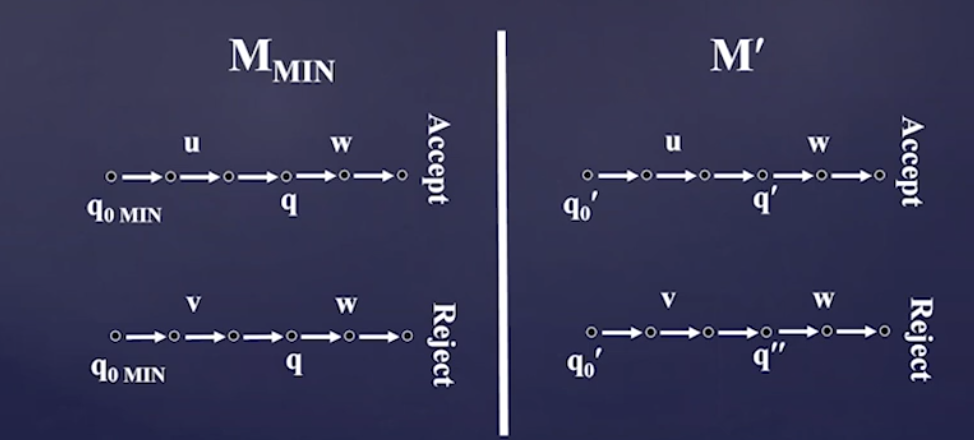
note that this is absurd because the same exact string $w$ caused accept and reject by pulling back the map in $M_{\min}$.