Setup: graphs are directed, and edges have “capacities”. We have source vertex \(s\) and sink vertex \(t\).
definitions
s-t cut
A cut is a s-t cuts is for a directed graph it goes from s’s side to t’s side; an edge cross an s-t cuts is the edges that goes from \(s\)’s side to \(t’s\) side
cut cost
the cut cost of an s-t cuts is the sum of the weights of the edges that cross the S-T cut.
minimum cut
an s-t cut with minimum cost.
flow
In addition to the weight of an edge, edges can also have a flow:
- the flow of an edge must be at most its capacity
- at each vertex, the incoming flow must equal to outgoing flow except for \(s\) and \(t\) nodes
The value of flows is the value of the flow out of \(s\), or the value of flows into \(t\) (those should equal)
maximum flow
The maximum valued flow.
max-flow-min-cut-theorem
The value of a max flow from \(s\) to \(t\) is equal to th e cost of a min \(st\) cut.
Suppose you can find s-t cut of cost \(X\), then you found an s-t flow of value \(X\). Then, those are both the min-cut and max-flow. This is because X >= min cut = max flow >= X, so X = min cut = max flow.
Intuition: the bottleneck to max-flow should be the min-cut.
Folk-Fulkerson Algorithm
ASSUME: no one-step loops \(a \leftrightarrow b\).
high level insights
- We’ll be updating a flow \(f\); start with \(f=0\)
- We will maintain a residual graph \(F_{f}\)
- A path from \(s\) to \(t\) with in \(G_{f}\) will give us a way to improve our flow \(f\)
- Continue until there’s no \(s\) \(t\) paths left.
residual graph
Suppose you have some flow on a graph, we make a residual graph with:
- update weight of each edge with (capacity - flow)
- for all \(u \to v\), add \(v \to u\) for which the weight is the value of flow
- remove all weight \(0\) edges
We call a path from \(s \to t\) in the residual graph an augmenting path.
key claim
If there is an augmenting path in the residual graph of \(G\) for flow \(f\); that is, \(\qty(s,t) \in G_{f}\), then we can increase the flow along that path in \(G\).
Casework:
Every \(s \to t\) path member in \(G_{f}\) is a forward edge in \(G\). We can just increase the flow along all edges by the minimum of the capacity of the path.
The \(s \to t\) path member in \(G_{f}\) contains backwards edges in \(G\). We can just increase the flow along all forward edges and decrease the flow along all backwards edges by the minimum of the capacity of the path
def increaseFlow(G_f: augmenting graph, f: flow):
p = stconn(G_f)
x = min_weight_on_any_edge(p)
for u,v in p:
if u,v in E(G):
f_new(u,v) = f(u,v) + x
if v,u in E(G):
f_new(u,v) = f(u,v) - x
return f_new
full-algorithm
def ford_fulkerson(G):
f = all_zero_flow()
G_f = G
while stconn(G_f): # for instance, BFS
f = increaseFlow(G_f, f)
G_f = augmenting_graph(G, f)
return f
how do we find minimum cut?
BFS along with \(s\) in the augmented graph; the algorithm above terminates when there’s no more path, so you will get a subset of the nodes. That’s the min cut.
how do we pick the paths to choose?
If we use BFS, we get \(O\qty(nm^{2})\) runtime, which is pretty good!
observe
If all capacities are integers, then the max flow in any max flow are also integers. i.e. we are adding / subtracting integers when we update each time. We start with \(0\), an integer, and we add/subtract integers.
uses
maximum bipartite matching
Match \(x_{1} … x_{n}\) to thing \(y_1 … y_{n}\), but each \(x_{j}\) may only want some subset of \(y\). We can setup a graph
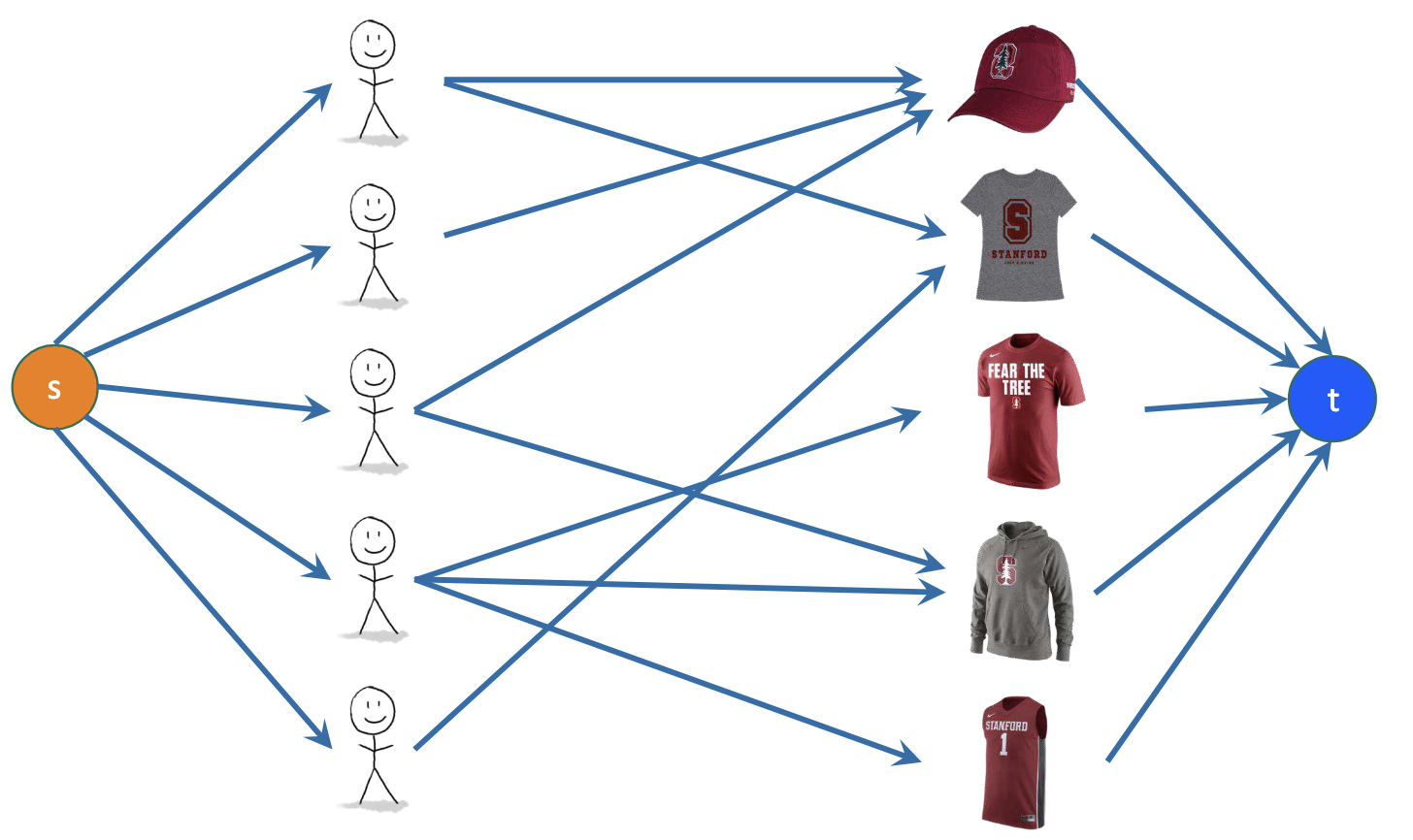
where all edges are 1. A maximum flow will give the maximum amount of happy matches (since each match has flow worth 1).
