probability of “or”
If its not possible for two events to happen at the same time, they are called mutually exclusive:
\begin{equation} P(E\ or\ F) = P(E)+P(F) - P(E \cap F) \end{equation}
This is called the inclusion exclusion principle. This is what motivates inclusion exclusion counting.
General inclusion exclusion principle
Its scary. Think about this:
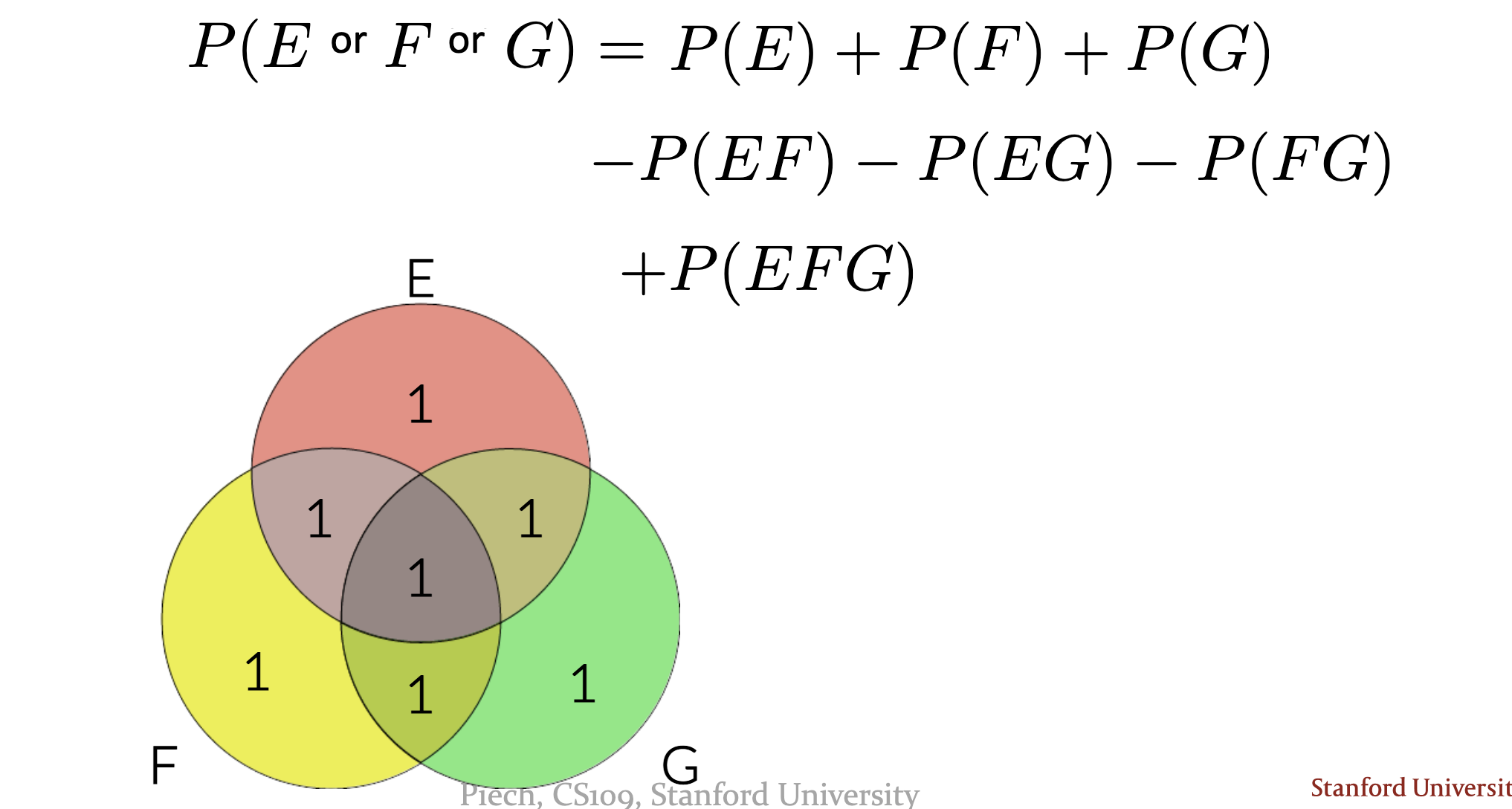
We basically need to alternate between adding and subtracting. (i.e.: in our case here, we add all the odd-group pairs (for P(x) and P(xyz)), we subtract the even-number pairs (for p(xy))).
And so:
\begin{equation} P(E_1\ or\ \dots\ or\ E_{n}) = \sum_{r=1}^{n} (-1)^{r+1} Y_{r} \end{equation}
whereby, \(Y_{j}\) is the sum of \(P(x_n, … x_{j})\) for combinations of \(j\) events.
Try not to do this.