Let’s begin. We want to create test for the linearity of a few assets, for whether or not they follow the CAPM.
Note that we will be using the Sharpe-Linter version of CAPM:
\begin{equation} E[R_{i}-R_{f}] = \beta_{im} E[(R_{m}-R_{f})] \end{equation}
\begin{equation} \beta_{im} := \frac{Cov[(R_{i}-R_{f}),(R_{m}-R_{f})]}{Var[R_{m}-R_{f}]} \end{equation}
Recall that we declare \(R_{f}\) (the risk-free rate) to be non-stochastic.
Let us begin. We will create a generic function to analyze some given stock.
We will first import our utilities
import pandas as pd
import numpy as np
Let’s load the data from our market (NYSE) as well as our 10 year t-bill data.
t_bill = pd.read_csv("./linearity_test_data/10yrTBill.csv")
nyse = pd.read_csv("./linearity_test_data/NYSEComposite.csv")
nyse.head()
Date Close
0 11/7/2013 16:00:00 9924.37
1 11/8/2013 16:00:00 10032.14
2 11/11/2013 16:00:00 10042.95
3 11/12/2013 16:00:00 10009.84
4 11/13/2013 16:00:00 10079.89
Excellent. Let’s load in the data for that stock.
def load_stock(stock):
return pd.read_csv(f"./linearity_test_data/{stock}.csv")
load_stock("LMT").head()
Date Close
0 11/7/2013 16:00:00 136.20
1 11/8/2013 16:00:00 138.11
2 11/11/2013 16:00:00 137.15
3 11/12/2013 16:00:00 137.23
4 11/13/2013 16:00:00 137.26
And now, let’s load all three stocks, then concatenate them all into a big-ol DataFrame.
# load data
df = { "Date": nyse.Date,
"NYSE": nyse.Close,
"TBill": t_bill.Close,
"LMT": load_stock("LMT").Close,
"TWTR": load_stock("TWTR").Close,
"MCD": load_stock("MCD").Close }
# convert to dataframe
df = pd.DataFrame(df)
# drop empty
df.dropna(inplace=True)
df
Date NYSE TBill LMT TWTR MCD
0 11/7/2013 16:00:00 9924.37 26.13 136.20 44.90 97.20
1 11/8/2013 16:00:00 10032.14 27.46 138.11 41.65 97.01
2 11/11/2013 16:00:00 10042.95 27.51 137.15 42.90 97.09
3 11/12/2013 16:00:00 10009.84 27.68 137.23 41.90 97.66
4 11/13/2013 16:00:00 10079.89 27.25 137.26 42.60 98.11
... ... ... ... ... ... ...
2154 10/24/2022 16:00:00 14226.11 30.44 440.11 39.60 252.21
2155 10/25/2022 16:00:00 14440.69 31.56 439.30 39.30 249.28
2156 10/26/2022 16:00:00 14531.69 33.66 441.11 39.91 250.38
2157 10/27/2022 16:00:00 14569.90 34.83 442.69 40.16 248.36
2158 10/28/2022 16:00:00 14795.63 33.95 443.41 39.56 248.07
[2159 rows x 6 columns]
Excellent. Now, let’s convert all of these values into daily log-returns (we don’t really care about the actual pricing.)
log_returns = df[["NYSE", "TBill", "LMT", "TWTR", "MCD"]].apply(np.log, inplace=True)
df.loc[:, ["NYSE", "TBill", "LMT", "TWTR", "MCD"]] = log_returns
df
Date NYSE TBill LMT TWTR MCD
0 11/7/2013 16:00:00 9.202749 3.263084 4.914124 3.804438 4.576771
1 11/8/2013 16:00:00 9.213549 3.312730 4.928050 3.729301 4.574814
2 11/11/2013 16:00:00 9.214626 3.314550 4.921075 3.758872 4.575638
3 11/12/2013 16:00:00 9.211324 3.320710 4.921658 3.735286 4.581492
4 11/13/2013 16:00:00 9.218298 3.305054 4.921877 3.751854 4.586089
... ... ... ... ... ... ...
2154 10/24/2022 16:00:00 9.562834 3.415758 6.087025 3.678829 5.530262
2155 10/25/2022 16:00:00 9.577805 3.451890 6.085183 3.671225 5.518577
2156 10/26/2022 16:00:00 9.584087 3.516310 6.089294 3.686627 5.522980
2157 10/27/2022 16:00:00 9.586713 3.550479 6.092870 3.692871 5.514879
2158 10/28/2022 16:00:00 9.602087 3.524889 6.094495 3.677819 5.513711
[2159 rows x 6 columns]
We will now calculate the log daily returns. But before—the dates are no longer relavent here so we drop them.
df
Date NYSE TBill LMT TWTR MCD
0 11/7/2013 16:00:00 9.202749 3.263084 4.914124 3.804438 4.576771
1 11/8/2013 16:00:00 9.213549 3.312730 4.928050 3.729301 4.574814
2 11/11/2013 16:00:00 9.214626 3.314550 4.921075 3.758872 4.575638
3 11/12/2013 16:00:00 9.211324 3.320710 4.921658 3.735286 4.581492
4 11/13/2013 16:00:00 9.218298 3.305054 4.921877 3.751854 4.586089
... ... ... ... ... ... ...
2154 10/24/2022 16:00:00 9.562834 3.415758 6.087025 3.678829 5.530262
2155 10/25/2022 16:00:00 9.577805 3.451890 6.085183 3.671225 5.518577
2156 10/26/2022 16:00:00 9.584087 3.516310 6.089294 3.686627 5.522980
2157 10/27/2022 16:00:00 9.586713 3.550479 6.092870 3.692871 5.514879
2158 10/28/2022 16:00:00 9.602087 3.524889 6.094495 3.677819 5.513711
[2159 rows x 6 columns]
And now, the log returns! We will shift this data by one column and subtract.
returns = df.drop(columns=["Date"]) - df.drop(columns=["Date"]).shift(1)
returns.dropna(inplace=True)
returns
NYSE TBill LMT TWTR MCD
1 0.010801 0.049646 0.013926 -0.075136 -0.001957
2 0.001077 0.001819 -0.006975 0.029570 0.000824
3 -0.003302 0.006161 0.000583 -0.023586 0.005854
4 0.006974 -0.015657 0.000219 0.016568 0.004597
5 0.005010 -0.008476 0.007476 0.047896 -0.005622
... ... ... ... ... ...
2154 0.005785 0.004940 -0.023467 -0.014291 0.001349
2155 0.014971 0.036133 -0.001842 -0.007605 -0.011685
2156 0.006282 0.064420 0.004112 0.015402 0.004403
2157 0.002626 0.034169 0.003575 0.006245 -0.008100
2158 0.015374 -0.025590 0.001625 -0.015053 -0.001168
[2158 rows x 5 columns]
We are now ready to run the correlation study.
Let’s now subtract everything by the risk-free rate (dropping the rfr itself):
risk_free_excess = returns.drop(columns="TBill").apply(lambda x: x-returns.TBill)
risk_free_excess
NYSE LMT TWTR MCD
1 -0.038846 -0.035720 -0.124783 -0.051603
2 -0.000742 -0.008794 0.027751 -0.000995
3 -0.009463 -0.005577 -0.029747 -0.000307
4 0.022630 0.015875 0.032225 0.020254
5 0.013486 0.015952 0.056372 0.002854
... ... ... ... ...
2154 0.000845 -0.028406 -0.019231 -0.003591
2155 -0.021162 -0.037975 -0.043738 -0.047818
2156 -0.058138 -0.060308 -0.049017 -0.060017
2157 -0.031543 -0.030593 -0.027924 -0.042269
2158 0.040964 0.027215 0.010537 0.024422
[2158 rows x 4 columns]
Actual Regression
It is now time to perform the actual linear regression!
import statsmodels.api as sm
Let’s work with Lockheed Martin first, fitting an ordinary least squares. Remember that the OLS functions reads the endogenous variable first (for us, the return of the asset.)
# add a column of ones to our input market excess returns
nyse_with_bias = sm.add_constant(risk_free_excess.NYSE)
# perform linreg
lmt_model = sm.OLS(risk_free_excess.LMT, nyse_with_bias).fit()
lmt_model.summary()
OLS Regression Results
==============================================================================
Dep. Variable: LMT R-squared: 0.859
Model: OLS Adj. R-squared: 0.859
Method: Least Squares F-statistic: 1.312e+04
Date: Mon, 31 Oct 2022 Prob (F-statistic): 0.00
Time: 10:39:24 Log-Likelihood: 6318.9
No. Observations: 2158 AIC: -1.263e+04
Df Residuals: 2156 BIC: -1.262e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0004 0.000 1.311 0.190 -0.000 0.001
NYSE 0.9449 0.008 114.552 0.000 0.929 0.961
==============================================================================
Omnibus: 423.969 Durbin-Watson: 1.965
Prob(Omnibus): 0.000 Jarque-Bera (JB): 11575.074
Skew: -0.160 Prob(JB): 0.00
Kurtosis: 14.341 Cond. No. 29.6
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Based on the constants row, we can see that—within \(95\%\) confidence—the intercept is generally \(0\) and CAPM applies. However, we do see a slight positive compared to the market. Furthermore, we can see that the regression has a beta value of \(0.9449\) — according the CAPM model, it being slightly undervarying that the market.
We can continue with the other stocks.
# perform linreg
mcd_model = sm.OLS(risk_free_excess.MCD, nyse_with_bias).fit()
mcd_model.summary()
OLS Regression Results
==============================================================================
Dep. Variable: MCD R-squared: 0.887
Model: OLS Adj. R-squared: 0.887
Method: Least Squares F-statistic: 1.697e+04
Date: Mon, 31 Oct 2022 Prob (F-statistic): 0.00
Time: 10:39:24 Log-Likelihood: 6551.1
No. Observations: 2158 AIC: -1.310e+04
Df Residuals: 2156 BIC: -1.309e+04
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0003 0.000 1.004 0.315 -0.000 0.001
NYSE 0.9651 0.007 130.287 0.000 0.951 0.980
==============================================================================
Omnibus: 323.911 Durbin-Watson: 1.988
Prob(Omnibus): 0.000 Jarque-Bera (JB): 3032.550
Skew: 0.395 Prob(JB): 0.00
Kurtosis: 8.753 Cond. No. 29.6
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Same thing as before, we are within \(95\%\) confidence having a intercept of \(0\) (with a slight positive edge), and it looks like MacDonald’s vary a little bit more than Lockheed Martin. The food industry is probably a tougher business than that in defense.
Lastly, to analyze the recently delisted Twitter!
# perform linreg
twtr_model = sm.OLS(risk_free_excess.TWTR, nyse_with_bias).fit()
twtr_model.summary()
OLS Regression Results
==============================================================================
Dep. Variable: TWTR R-squared: 0.522
Model: OLS Adj. R-squared: 0.522
Method: Least Squares F-statistic: 2357.
Date: Mon, 31 Oct 2022 Prob (F-statistic): 0.00
Time: 10:39:24 Log-Likelihood: 4307.1
No. Observations: 2158 AIC: -8610.
Df Residuals: 2156 BIC: -8599.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const -0.0002 0.001 -0.346 0.730 -0.002 0.001
NYSE 1.0173 0.021 48.549 0.000 0.976 1.058
==============================================================================
Omnibus: 661.205 Durbin-Watson: 1.986
Prob(Omnibus): 0.000 Jarque-Bera (JB): 15925.609
Skew: -0.883 Prob(JB): 0.00
Kurtosis: 16.191 Cond. No. 29.6
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Evidently, Twitter is much more variable. It looks like it has a nontrivial bias (the intercept being -0.001 being within the \(95\%\) confidence band — that the security is possibly significantly underperforming the CAPM expectation in the market.) Furthermore, we have a positive beta value: that the asset is more variable than the market.
manual regression
We can also use the betas formula to manually calculate what we expect for the beta values (i.e. as if they were one IID random variable.)
risk_free_cov = risk_free_excess.cov()
risk_free_cov
NYSE LMT TWTR MCD
NYSE 0.001143 0.001080 0.001163 0.001103
LMT 0.001080 0.001188 0.001116 0.001083
TWTR 0.001163 0.001116 0.002264 0.001155
MCD 0.001103 0.001083 0.001155 0.001200
Finally, to construct the beta values. Recall that:
\begin{equation} \beta_{im} := \frac{Cov[(R_{i}-R_{f}),(R_{m}-R_{f})]}{Var[R_{m}-R_{f}]} \end{equation}
and that:
\begin{equation} Var[X] = Cov[X,X], \forall X \end{equation}
# get the market variance (covariance with itself)
market_variation = risk_free_cov.NYSE.NYSE
# calculate betas
betas = {"LMT": (risk_free_cov.LMT.NYSE/market_variation),
"TWTR": (risk_free_cov.TWTR.NYSE/market_variation),
"MCD": (risk_free_cov.MCD.NYSE/market_variation)}
# and make dataframe
betas = pd.Series(betas)
betas
LMT 0.944899
TWTR 1.017294
MCD 0.965081
dtype: float64
Apparently, all of our assets swing less than the overall NYSE market! Especially Lockheed—it is only \(94.4\%\) of the market variation. Furthermore, it is interesting to see that Twitter swings much more dramatically compared to the market.
Fund creation
We will now create two funds with the three securities, one with equal parts and one which attempts to maximizes the bias (max returns) while minimizing the beta variance value compared to the market.
“Equal-Parts Fund” (“Fund 1”)
We will now create a fund in equal parts. Here it is:
fund_1_returns = returns.LMT + returns.TWTR + returns.MCD
fund_1_returns
1 -0.063167
2 0.023420
3 -0.017149
4 0.021384
5 0.049750
...
2154 -0.036409
2155 -0.021132
2156 0.023917
2157 0.001720
2158 -0.014596
Length: 2158, dtype: float64
We will calculate the excess returns of this fund:
fund_1_excess = fund_1_returns-returns.TBill
fund_1_excess
1 -0.112813
2 0.021600
3 -0.023310
4 0.037041
5 0.058226
...
2154 -0.041349
2155 -0.057265
2156 -0.040503
2157 -0.032449
2158 0.010994
Length: 2158, dtype: float64
And then perform a regression
# perform linreg
fund_1_model = sm.OLS(fund_1_excess, nyse_with_bias).fit()
fund_1_model.summary()
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.473
Model: OLS Adj. R-squared: 0.473
Method: Least Squares F-statistic: 1935.
Date: Mon, 31 Oct 2022 Prob (F-statistic): 3.01e-302
Time: 10:39:24 Log-Likelihood: 3869.5
No. Observations: 2158 AIC: -7735.
Df Residuals: 2156 BIC: -7724.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.0007 0.001 0.841 0.401 -0.001 0.002
NYSE 1.1290 0.026 43.993 0.000 1.079 1.179
==============================================================================
Omnibus: 600.456 Durbin-Watson: 2.022
Prob(Omnibus): 0.000 Jarque-Bera (JB): 8416.514
Skew: -0.914 Prob(JB): 0.00
Kurtosis: 12.501 Cond. No. 29.6
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Surprisingly, we have now created a significantly riskier investment that, though riskier, generates a much higher probability of reward (\(+0.001\) is now within the \(99\%\) band!)
A Better Fund
To me, this is the payoff of this assignment. We will now use CAPM to create the “best” fund combination—given some variance, the funds which match CAPM. To do this, let’s create a generic linear combination of the assets.
import sympy as sym
x = sym.Symbol('x')
y = sym.Symbol('y')
z = sym.Symbol('z')
fund_2_returns = x*returns.LMT + y*returns.TWTR + z*returns.MCD
fund_2_returns
1 0.0139260753744255*x - 0.0751364261353569*y - ...
2 -0.00697525170622448*x + 0.0295704573211193*y ...
3 0.000583132897928884*x - 0.0235859990058791*y ...
4 0.000218587198947517*x + 0.016568426347233*y +...
5 0.00747599199607762*x + 0.0478955096700351*y -...
...
2154 -0.0234665578621085*x - 0.0142913301107561*y +...
2155 -0.00184214468578059*x - 0.0076045993852194*y ...
2156 0.00411172646842317*x + 0.0154024001854269*y +...
2157 0.00357547337231878*x + 0.0062445563228315*y -...
2158 0.00162509910496933*x - 0.0150529686289622*y -...
Length: 2158, dtype: object
Excellent. We will also calculate the excess returns of this fund:
fund_2_excess = fund_2_returns-returns.TBill
Y = fund_2_excess.to_numpy()
Y
[0.0139260753744255*x - 0.0751364261353569*y - 0.00195664549320096*z - 0.0496463208073039
-0.00697525170622448*x + 0.0295704573211193*y + 0.000824317408861575*z - 0.00181917459665826
0.000583132897928884*x - 0.0235859990058791*y + 0.00585367525146019*z - 0.00616055581298536
...
0.00411172646842317*x + 0.0154024001854269*y + 0.00440300114913317*z - 0.0644196927849867
0.00357547337231878*x + 0.0062445563228315*y - 0.0081004573348249*z - 0.0341688956152497
0.00162509910496933*x - 0.0150529686289622*y - 0.00116834209450634*z + 0.0255902303732043]
We cast this type to a numpy array because we are about to perform some matrix operations upon it.
Now, let us perform the actual linear regression ourselves. Recall that the pseudoinverse linear regression estimator is:
\begin{equation} \beta = (X^{T}X)^{-1}X^{T}Y \end{equation}
We have already our \(Y\) as a vector (above), and our \(X\) is:
X = nyse_with_bias.to_numpy()
X
[[ 1.00000000e+00 -3.88457302e-02]
[ 1.00000000e+00 -7.42217926e-04]
[ 1.00000000e+00 -9.46284244e-03]
...
[ 1.00000000e+00 -5.81378271e-02]
[ 1.00000000e+00 -3.15429207e-02]
[ 1.00000000e+00 4.09643405e-02]]
We now have our matrices, let’s perform the linear regression!
linear_model = np.linalg.inv((X.transpose()@X))@X.transpose()@Y
linear_model
[0.000544056413840724*x - 6.62061061591867e-5*y + 0.000429966553373172*z - 0.000178620725465344
0.0457830563134785*x + 0.118178191274045*y + 0.0659651260604729*z + 0.899115719100281]
Excellent. So we now have two rows; the top row represents the “bias”—how much deviation there is from CAPM, and the bottom row represents the “rate”—the “beta” value which represents how much excess variance there is.
We can will solve for a combination of solutions to give us specific values of returns vs risk. We will set the asset to learn exactly as much as the market (i.e. no bias).
deviance_expr = linear_model[0]
deviance_expr
0.000544056413840724*x - 6.62061061591867e-5*y + 0.000429966553373172*z - 0.000178620725465344
We will now try to make variance exactly as much as that in the market.
risk_expr = linear_model[1] - 1
risk_expr
0.0457830563134785*x + 0.118178191274045*y + 0.0659651260604729*z - 0.100884280899719
Let us now calculate the boundary condition of our optimization problem by solving an expression in these two expressions.
solution = sym.solvers.solve([deviance_expr, risk_expr], x,y,z)
solution
{x: 0.412737013327711 - 0.819584899551304*z, y: 0.693765220909132 - 0.24067066980814*z}
Excellent. Let us recalculate our optimization objective (“deviance”—return) in terms of these new solutions. We aim now to maximize this expression by minimizing (i.e. our optimizer minimizes) the negative thereof—recalling that scypy works as a minimizer.
optim_objective = deviance_expr.subs(solution)-1e2
optim_objective
-5.04831636563563e-19*z - 100.0
We can now use this value to solve for a \(z\) value.
optim_solution = sym.solvers.solve([optim_objective], z)
optim_solution
{z: -1.98085842402250e+20}
Excellent. We can now solve for the rest of our values.
z0 = float(optim_solution[z])
x0 = solution[x].subs(z, z0)
y0 = solution[y].subs(z, z0)
(x0,y0,z0)
(1.62348165247784e+16, 4.76734523704593e+15, -1.980858424022502e+16)
This would create the following plan:
# solution
fund_2_nobias = x0*returns.LMT + y0*returns.TWTR + z0*returns.MCD
fund_2_nobias.mean()
0.009168283711770158
Recall that this is the performance of the balanced portfolio:
fund_1_returns.mean()
0.0009224705380695683
Finally, let’s plot the prices of our various funds:
import matplotlib.pyplot as plt
import matplotlib.dates as mdates
import seaborn as sns
from datetime import datetime
sns.set()
fund_2_price = x0*df.LMT + y0*df.TWTR + z0*df.MCD
fund_1_price = df.LMT + df.TWTR
fund_l_price = df.LMT
fund_t_price = df.TWTR
dates = df.Date.apply(lambda x:datetime.strptime(x, "%m/%d/%Y %H:%M:%S"))
sns.lineplot(x=dates, y=fund_2_price.apply(sym.Float).astype(float))
sns.lineplot(x=dates, y=fund_1_price.apply(sym.Float).astype(float))
sns.lineplot(x=dates, y=fund_l_price.apply(sym.Float).astype(float))
sns.lineplot(x=dates, y=fund_t_price.apply(sym.Float).astype(float))
plt.gca().xaxis.set_major_locator(mdates.YearLocator())
plt.gca().xaxis.set_major_formatter(mdates.DateFormatter('%Y'))
plt.gca().set_ylabel("Price")
plt.show()
None
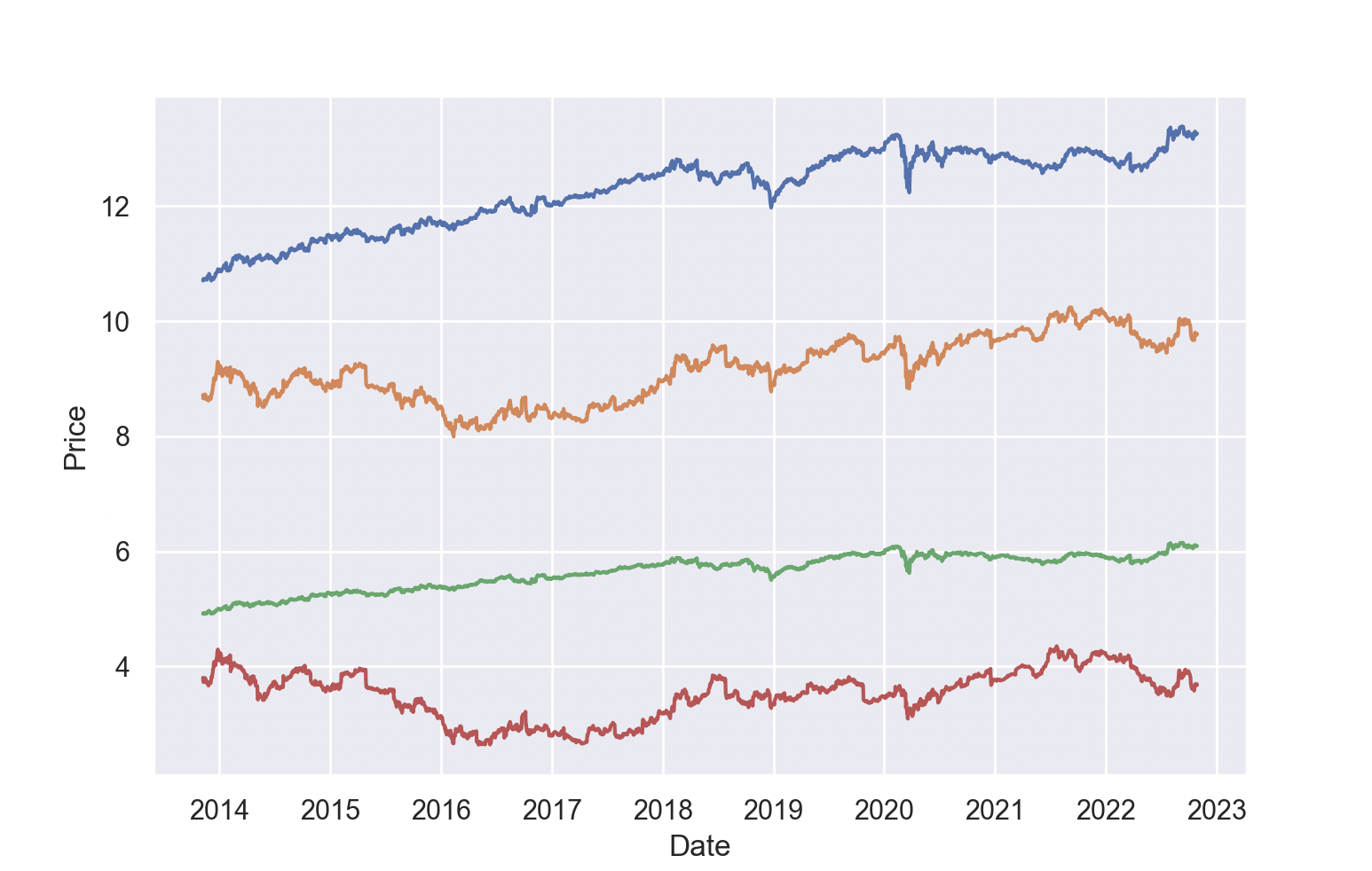
Recall that we didn’t actually buy any MacDonald’s. So, we have—blue, being our “optimal” portfolio, yellow, our balanced portfolio, green, being Lockheed, and red, being Twitter.
Our portfolio works surprisingly well!