Dot product
Calculations
Let’s calculate some dot products!
\begin{equation} \begin{pmatrix} 1 \\ 0 \end{pmatrix} \cdot \begin{pmatrix} 0 \\ 1 \end{pmatrix} = 0 \end{equation}
\begin{equation} \begin{pmatrix} 1 \\2 \end{pmatrix} \cdot \begin{pmatrix} 2 \\1 \end{pmatrix} = 4 \end{equation}
\begin{equation} \begin{pmatrix} 1 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} -1 \\1 \end{pmatrix} = 0 \end{equation}
\begin{equation} \begin{pmatrix} 1 \\1 \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 2 \end{pmatrix} = 4 \end{equation}
Interpretation
Geometrically, the intepretation of the dot product is the magnitude that comes from scaling the bottom projected value by the top value. This is essentially multiplying the proportion of one vector that’s parallel to the other by each other.
Cross Product
Calculations
Cross products!
\begin{equation} \begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix} \times \begin{pmatrix} -1 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 \\ -1 \\0 \end{pmatrix} \end{equation}
\begin{equation} \begin{pmatrix} 1 \\ 1 \\ -1 \end{pmatrix} \times \begin{pmatrix} 0 \\ 0 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \\ -2 \\0 \end{pmatrix} \end{equation}
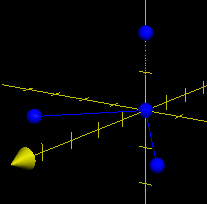
The dot product is the point that is perpendicular to the other two input vectors.
Why its not a field
We want to check why the multiplication of vectors in \(\mathbb{F}^{3}\) via taking the cross product cannot form a field.
We can safely assume that the addition operation of the vectors derive their closure, commutativity, associativity from these properties in \(\mathbb{F}\).
Therefore, we will verify these properties with multiplication. The only closed multiplication-like operation of vectors is the cross-product. Let’s first define the cross-product.
Given two vectors in \(\mathbb{F}^{3}\):
\begin{equation} \begin{pmatrix} a \\b \\ c \end{pmatrix}, \begin{pmatrix} d \\ e\\f \end{pmatrix} \end{equation}
Their cross product is the vector in \(\mathbb{F}^{3}\) defined by:
\begin{equation} \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a & b & c \\ d & e & f \end{vmatrix} \end{equation}
Taking the actual determinant, we have that:
\begin{equation} \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a & b & c \\ d & e & f \end{vmatrix} = \begin{pmatrix} bf-ce \\ dc-af \\ ac-db \end{pmatrix} \end{equation}
Identity
Let’s first figure the identity of this operation. We wish to figure some \((a,b,c)\) such that the result of the cross product would be \((d,e,f)\).
Geometrically, the perpendicularity of a vector is the resulting value of the cross product; however, no vector (apart from \(\vec{0}\)) can be perfectly perpendicular to itself exactly. This would indicate that no such identities exist.
We can also observe that there is no \(f\) term on the bottom of the cross product. This would indicate that no combination of \((a,b,c)\) can construct the needed \(f\) on the last entry.
Finally, for a more formal proof.
Proof: there can not exist a field-like identity for a cross product.
For the sake of contradiction let’s say for some nonzero vector \(\vec{v} \in \mathbb{F}^{3}\), there exists some identity named \(\vec{e} \in \mathbb{F}^{3}\) that follows the properties of identities in a field.
We first have that:
\begin{equation} \vec{e} \times \vec{v} = \vec{v} \end{equation}
by the definition of the identity.
And also that:
\begin{equation} \vec{v} \times \vec{e}= \vec{v} \end{equation}
by the fact that field-like operations commutes.
We have also the property of cross products that:
\begin{align} &\vec{a} \times \vec{b} = -(\vec{b} \times \vec{a}) \\ \Rightarrow\ & \vec{a} \times \vec{b} + \vec{b} \times \vec{a} = 0 \end{align}
By applying the inverse of \(-(\vec{b}\times \vec{a})\) to both sides, as cross products are closed and therefore an additive inverse exists.
Therefore, we have that:
\begin{equation} \vec{v} + \vec{v} = 0 \end{equation}
We see then \(\vec{v}\) is its own additive inverse. Therefore \(\vec{v}\) itself is also \(0\). But we established that \(\vec{v}\) can be non-zero. Reaching contradiction, \(\blacksquare\). (this is iffy)
Commutativity
Because of the fact that two-by-two matricies exists on the diagonals, the cross product is also not commutative. In fact,
Determinants
The geometric interpretation of the determinants is the change in area inside a vector which it stretches a given vector.