Factoids:
- \((AB)^{*} = B^{*} A^{*}\), \((A+B)^{*} = A^{*} + B^{*}\)
An unitary operator is invertible, and the inverse of its matrix representation is its transpose
Take \(M\) an unitary square matrix, with orthonormal columns. Note that this matrix, by construction, sends each basis \(v_{j}\) to $ej$—a set of \(dim\ V\) (as there are \(dim\ V\) columns to \(M\)) linearly independent (as \(e_{j}\), through orthonormality, are linearly independent) vectors. As we have \(dim\ V\) linearly independent vectors, the \(e_{j}\) form a basis. As each \(v_{j}\) is sent to $ej$—both a basis of $V$—we note that the finite-dimensional operator corresponding to \(M\) is subjective and hence invertible.
Construct now the matrix \(M^{*}\). Consider \(M M^{*}\). Note that the multiplication operation will require taking the inner product of each row of \(M\), against each column of \(M^{*}\); that is, this operation will result in taking the inner products between each pair of orthonormal columns of \(M\).
Recall that, per the definition of orthonormal vectors, for a pair of vectors \(e_{i}, e_{j}\), \(\langle e_{i}, e_{j} \rangle = 0\) for \(i \neq j\) and \(=1\) for \(i=j\). Therefore, this row-column product will be \(1\) when row \(j\) and column \(j\) is multiplied together and \(0\) otherwise.
In this fashion, \(M M^{*} =I\); in a similar fashion, \(M^{*} M = I\). Therefore, \(M^{*} = M^{-1}\).
Result 2: unitary matricies are normal
Recall the matrix \(M\) is normal if \(A A^{*} = A^{*} A\). Now, recall that for a unitary operator \(A^{*} = A^{-1}\).
Now, we have that:
\begin{equation} A A^{*} = A A^{-1} = I = A^{-1} A = A^{*}A \end{equation}
Result 3: self-adjoint matricies are normal
Recall a self-adjoint matrix acts like \(A = A^{*}\).
Now:
\begin{equation} A A^{*} = A A = A^{*} A \end{equation}
Observation 1: some matricies are both self-adjoint and unitary
Take the symmetric matrix formed by conjoining each of the standard bases of euclidian space \(\mathbb{F}^{n}\). That is, the identity matrix.
The matrix has orthonormal columns (as the standard bases are orthonormal), and self-adjoint as it is symmetric.
Problem 1: Venn Diagram
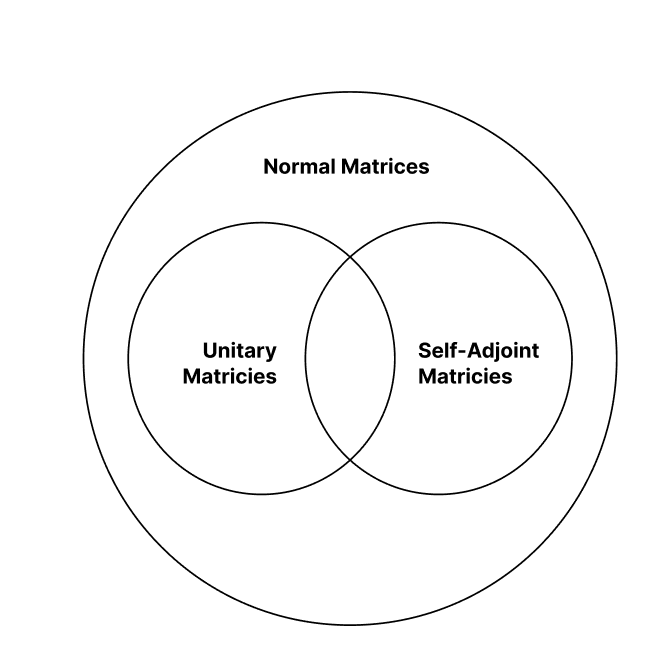
Per results above.
Problem 2: Group!
Self-Adjoint
Not closed under multiplication:
\begin{equation} \mqty(a & b \\ b & c) \mqty(f & g \\ g& h) = \mqty(af + bg & ag+bh \\ bf+cg & bg+ch) \end{equation}
Evidently, this matrix is no longer symmetric (i.e. not self adjoint).
Unitary
Do form a group!
Normal
There’s no inverse for \(0\).
Is this proof taking too much of a shortcut? / Wishywashy.
By the complex spectral theorm, \(T\) being normal implies that there is an orthonormal bases of eigenvalues of \(T\) (i.e. there is a diagonal representation of \(T\)). This can be obtained with Schur’s theorem, then applying the condition that \(A A^{*} = A^{*}A\) to show that the “upper-triangular” matrix formed by the orthonormal bases is actually diagonal.
By calculation, diagonal matricies’ multiplication is closed.
We now inherit the identity and associativity from general matricies.
So invertible normal matricies form a group.
“Matrix Adjoint”
\(A^{*}\) is the adjoint of the matrix.
That:
\begin{equation} \langle Tv,w \rangle = \langle v, T^{*}w \rangle \end{equation}

- \(A = A^{*} \implies \lambda_{i} \in \mathbb{R}\)
- \(A^{*} A = A A^{*} \implies\) diagonalizable based on an orthonormal basis of eigenvectors
- \(A\) is orthogonal/unitary \(\implies\) \(A^{*} = A^{-1}\)
7.13: E.v. of self-adjoint operators are real.
7.14: Over \(\mathbb{C}\), \(Tv\) is orthogonal to all \(v\) IFF \(T\) is the zero matrix
7.16: Over \(\mathbb{R}\), \(Tv\) is orthogonal to all \(v\) and \(T\) is self-adjoint, then \(T\) is the zero matrix
7.22: eigenvectors of \(T\) corresponding to distinct eigenvalues are orthogonal if \(T \in \mathcal{L}(V)\) is normal.
Also 7.24: the spectral theorem—that if \(T\) is normal, then \(V\) has an orthonormal basis of eigenvectors of \(T\) and so \(T\) is diagonalizable with respect to an orthonormal basis
Recall “normal”: \(A A^{*} = A^{*} A\)