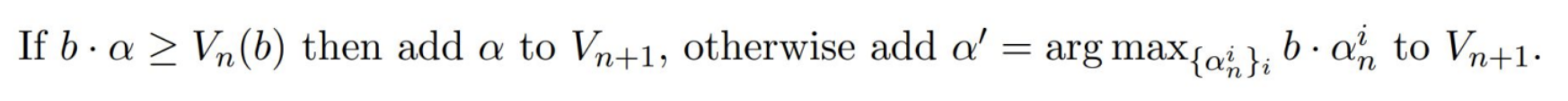The number of alpha vectors needed to perform PBVI is one for each of your belief sample. Which is a bad idea. Perseus is essentially PBVI, where this idea is explored slightly.
The preamble is the same as PBVI:
we keep track of a bunch of alpha vectors and belief samples (which we get from point selection):
\begin{equation} \Gamma = \{\alpha_{1}, \dots, \alpha_{m}\} \end{equation}
and
\begin{equation} B = \{b_1, \dots, b_{m}\} \end{equation}
To preserve the lower-boundedness of these alpha vectors, one should seed the alpha vectors via something like blind lower bound
We can estimate our utility function at any belief by looking in the set for the most optimal:
\begin{equation} U^{\Gamma}(b) = \max_{\alpha \in \Gamma} \alpha^{\top}b \end{equation}
We now define a function named backup (see PBVI Backup), and call it on ONLY ONE belief:
let us sample—
\begin{equation} b \in B \end{equation}
and call backup to get:
\begin{equation} \alpha’ = backup(\Gamma, b) \end{equation}
where,
\begin{equation} backup(\Gamma, b) \rightarrow \alpha_{t+1} \end{equation}
Now, if \(b \cdot a’ > \max_{\alpha \in \Gamma} \alpha^{\top}b\) (i.e. we just increased our value floor because our new alpha vector indicates a higher value at \(b\)), we add our new vector to the set \(\Gamma\). Otherwise, we add \(a’ = \arg\max_{\alpha \in \Gamma} b \cdot \alpha\), the alpha vector which previously got the highest value for \(b\).
After this, we pull a Perseus-core funni:
Perseus Belief Pruning
let us define:
\begin{equation} V_{t}(b) = \max_{\alpha \in \Gamma_{t}} \alpha \cdot b \end{equation}
and
\begin{equation} V_{t+1}(b) = \max_{\alpha \in \Gamma_{t+1}} \alpha \cdot b \end{equation}
namely, the expected value of \(b\) before and after belief updates. Then, we:
\begin{equation} B_{t+1} = \{b \in B, \text{if}\ V_{t+1}(b) < V(b)\} \end{equation}
that is, if updating our sampled belief’s alpha vector improved the value of another belief in the set by accident already, we don’t need to update that belief again.
Repeat this process until we are out of beliefs to update, that is, when \(B = \emptyset\).
Slight Variation?
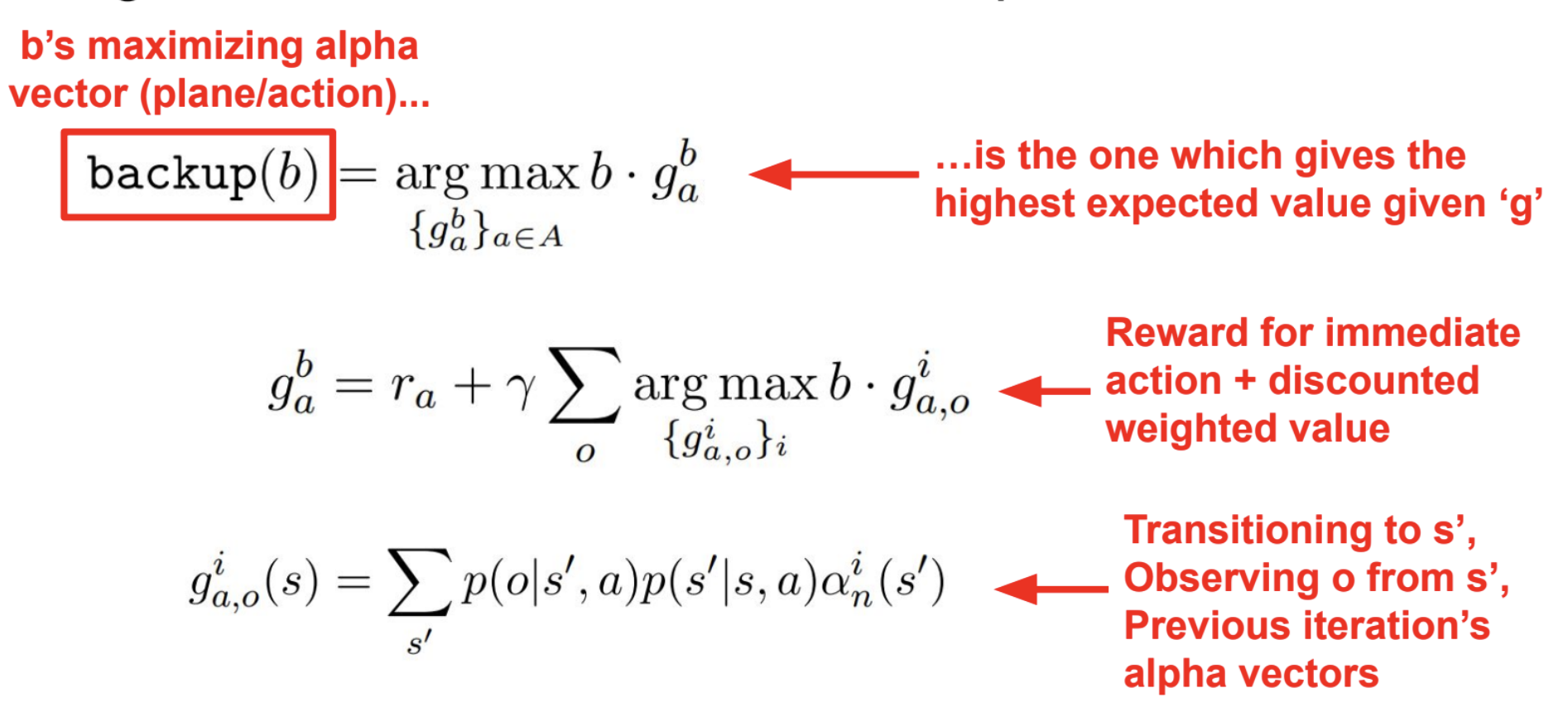
then,