A high level sketch:
Another High Level Sketch
Step 1: Write some RegExps
Do that.
Step 2: Construct R
For regular expressions you have defined for keywords, identifies, numbers, etc… We want to construct an uber union regular expression:
\begin{align} R &= \text{Keyword} + \text{Identifier} + \text{Number} + \dots \\ &= R_1 | R_2 | R_3 | \dots \end{align}
Step 3: Tokenization
For input \(x_1, …, x_{n}\), for \(i \in 1 …n\) inclusive, we check:
\begin{equation} x_1 \dots x_{i} \stackrel{?}{\in} L\qty( R) \end{equation}
Upon success for some \(i\), we know that \(x_{1}, …, x_{i} \in L\qty(R_{j})\) for some \(j\). We can then send \(x_1, …, x_{i}\) to the parser and then continue lexing for input \(x_{i+1}…x_{n}\).
ambiguity
- multiple matches, different lengths: we pick the longest possible substring
- multiple matches, same length: pick the first rule
- nothing matches: we just put a catch all rule in the bottom
How exactly does “matching” mean?
DFAs, NFAs, subset construction! Conventions used in this class:
- \(\Sigma\) alphabet
- \(S\) states
- \(n\) start
- \(F \subseteq S\) accepting states
- \(S \to^{x} S\) transition
and recall regular expressions are equivalent to regular languages. When you attempt to take a transition that doesn’t exist in NFAs, you end into nothing.
algorithm for casting RegExp to NFA
By convention every NFA will have a single starting state and a single ending state. We will then compose every composition’s machine together.
concatenation
For parser of \(A\) and \(B\), we compose them by composing the accept state of \(A\) with an \(\epsilon\) move to \(B\), and make \(A\) no longer an accepting state.

union
We make an epsilon move from the starting state to both \(A\) and \(B\). And then when you hit the accepting state of either \(A\) or \(B\) you epsilon move to the accepting state.
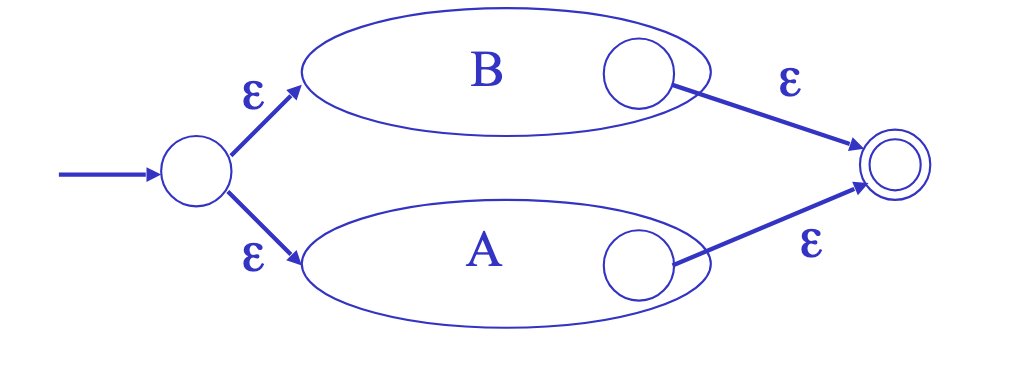
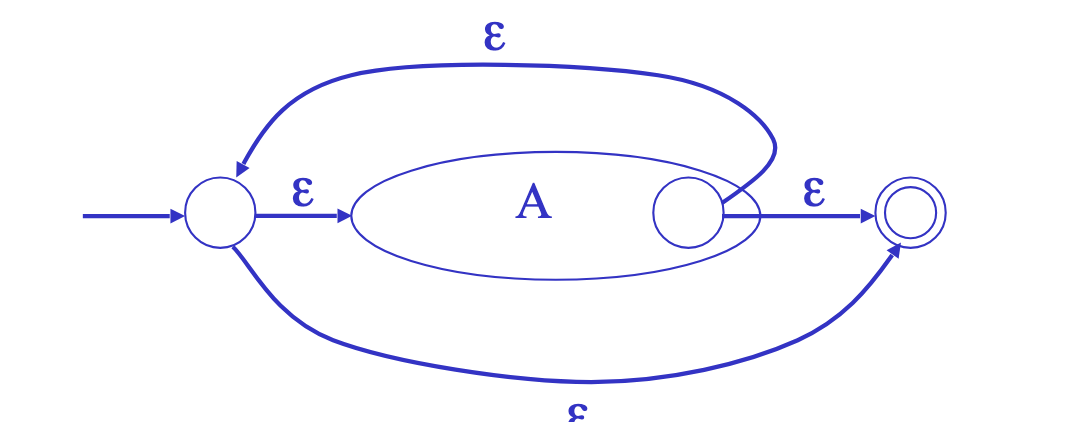
kleene star
implementing DFAs as a table
- columns: alphabet
- rows: states
the way you implement this is to just look up the (state, symbol) pair, take the transition, and look up the new state, symbol, etc.
| 0 | 1 | |
|---|---|---|
| a | a | b |
| b | a | b |
is
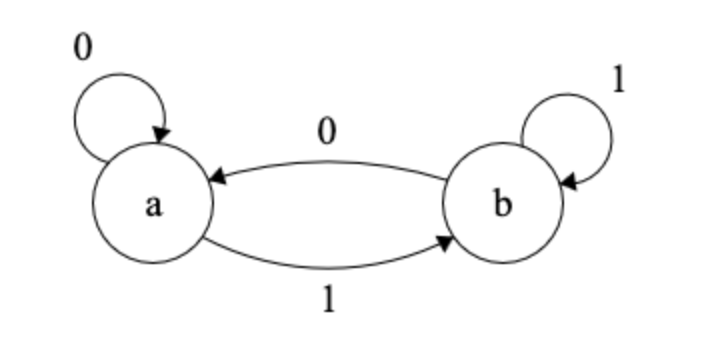
and so on. To construct this table, you just read off the transition function.
