a randomized turing machine is a turing machine with functions \(\delta_{0}\), \(\delta_{1}\). During computation, we take either \(\delta_{0}\) or \(\delta_{1}\) each with probability \(\frac{1}{2}\).
See also randomized algorithm.
decision
a randomized TM decides a particular language \(L\) if, \(\forall x \in \Sigma^{*}\), we have that:
\begin{align} &x \in L \implies \text{Pr}\qty [M\text{ accepts } x] \geq \frac{2}{3} \\ &x \not\in L \implies \text{Pr}\qty [M\text{ accepts } x] \leq \frac{1}{3} \end{align}
NOTE! we have to prove this for all \(x\). “most \(x\)” is not good enough.
alternate (“deterministic”) definition of randomized TM
Rather than having two transitions, you have a single transition + you add an auxiliary tape which is a tape filled with random values.
\(M\) looks at the real input and also, if it wants, consumes one of the random bits.
BPTIME
\begin{equation} \text{BPTIME}\qty(t\qty(n)) = \qty {L: \exists \text{randomized TM that decides $L$ in $O(t(n))$ time}} \end{equation}
in particular:
“decides in \(O\qty(t\qty(n))\) time” means:
\begin{equation} \max_{x; |x| = n} \max_{\text{outcomes of randomness}} \qty {\text{$M$ takes $t\qty(n)$ steps}} \end{equation}
funnily enough, \(\max\) and \(\mathbb{E}\) could be swapped here only up to (some?) slowdown.
BPP
\begin{equation} \text{BPP} = \text{BPTIME}\qty(\text{poly}\qty(n)) \end{equation}
RP
RP is the “one-sided error” class where we will always reject when not in the language and we will accept with some fixed probability.
look, a chart!
accept probability for…
| language | x in L | x not in L |
|---|---|---|
| BPP | >= 2/3 | <= 1/3 |
| BPP | 1-2-n | 2-n |
| P | 1 | 0 |
| RP (one-sided error) | >= 1/2 | 0 |
| RP (one-sided error) | 1-2-n | 0 |
| NP | > 0 | 0 |
RP is essentially “NP with a lot of witnesses”—you are really really certain (up to whatever probability you’d like, since RP success amplifies).
Notice that this makes…
RP in NP
\begin{equation} RP \subseteq NP \end{equation}
RP is “accept with high probability” and NP is “accept somehow”.
RP success amplification
if \(M\) is a one-sided error truing machine with error \(\leq \frac{1}{2}\), then just run \(M\) \(k\) times to obtain:
\begin{equation} 2^{-\theta\qty(k)} \end{equation}
failure probability. i.e. if the correct answer is accept, than the system will return accept for \(1 - 2^{-\theta\qty(k)}\) chance (with Big-oh so the base doesn’t matter).
BPP success amplification
You run our \(M\) in total \(k\) times and compute majority; if more than half accepts, then overall accept. If more than half rejects, then overall reject.
This is wrong with probability \(2^{-O\qty(k)}\), and correct with probability \(1-2^{-O\qty(k)}\) (with Big-oh so the base doesn’t matter).
Proof: suppose you flip a coin that’s H with probability \(\geq \frac{2}{3}\), and T with probability \(\leq \frac{1}{3}\). Flip coin \(k\) times; what’s the probability that you see more \(T\) than \(H\)?
\begin{equation} \sum_{l \geq \frac{k}{2}}^{} {k \choose l} \qty(\frac{2}{3})^{k-l} \qty(\frac{1}{3})^{l} \end{equation}
Since \(k = \frac{k}{2}\) is the maximize value of the content, we have:
\begin{align} &\sum_{l \geq \frac{k}{2}}^{} {k \choose l} \qty(\frac{2}{3})^{k-l} \qty(\frac{1}{3})^{l}\\ &\leq \qty(\frac{2}{3})^{\frac{k}{2}} \qty(\frac{1}{3})^{\frac{k}{2}} \sum_{k \geq \frac{k}{2}}^{} {k \choose l } \\ &\leq \qty(\frac{2}{3})^{\frac{k}{2}} \qty(\frac{1}{3})^{\frac{k}{2}} 2^{k} \\ &= \qty(\frac{8}{9})^{\frac{k}{2}} \\ &= 2^{-O\qty(k)} \end{align}
so our failure probability decreases exponentially.
randomness hierarchy
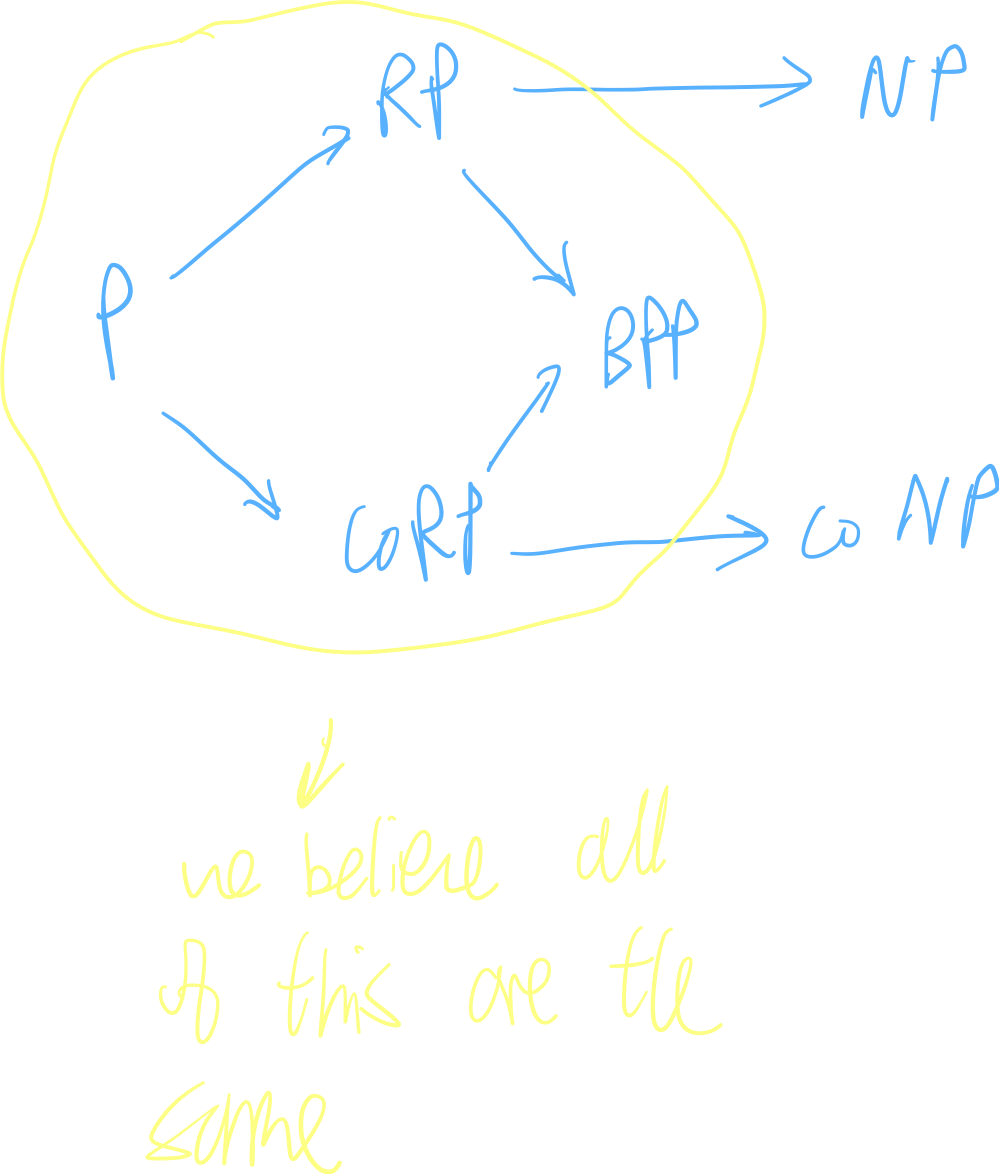
ZPP
\begin{equation} \text{ZPP}= \text{RP} \cap \text{coRP} \end{equation}
We will prove on the set that \(\text{ZPP}\) is a class of recognized by randomized Turing Machine that never errors, but runs in expected polynomial time.
every polytime randomized algorithm can be derandomized in exponential time
first, an alternate BPP definition
\begin{equation} L \in \text{BPP}\text{ if } \exists det\text{ polytime TM $M$, with} \end{equation}
- tape \(x \in \qty {0,1}^{*}\) “real input”
- tape \(v \in \qty {0,1}^{\text{poly}\qty(|x|)}\), random bits
\begin{equation} \forall x \in L, \text{Pr}_{r \in \qty {0,1}^{\text{poly} \qty(|x|)}} \qty[ M\qty(x,r), \text{acc}] \geq \frac{2}{3} \end{equation}
\begin{equation} \forall x \not \in L, \text{Pr}_{r \in \qty {0,1}^{\text{poly} \qty(|x|)}} \qty[ M\qty(x,r), \text{acc}] \leq \frac{1}{3} \end{equation}
next, we show \(\text{BPP} \subseteq \text{EXP}\)
Because we can show this by simply brute forcing \(r \sim \qty {0,1}^{\text{poly}\qty(|x|)}\), simulate \(M\qty(x,r)\); keep track (count) accept, reject, etc. and then just compute the values above.