a language \(L’\) is a regular language if there exists some DFA \(M\) such that \(L’ = L(M)\).
additional information
a proper subset
a proper subset of a regular language isn’t necessarily regular
regular expressions are equivalent to regular languages
see regular expressions are equivalent to regular languages
properties of regular languages
union
union of two languages includes all strings in a or b:
\begin{align} A \cup B = \qty {w | w \in A\ OR\ w \in B } \end{align}
intersection
union of two languages includes all strings in a and b:
\begin{align} A \cap B = \qty {w | w \in A\ AND\ w \in B } \end{align}
complement
complement of two languages includes all strings which isn’t in that language:
\begin{align} \neg A = \qty {w \in \Sigma^{*} | w \not \in A} \end{align}
reverse
stuff said backwards!
\begin{align} A^{R} = \qty {(w_{1} \dots w_{k}) | (w_{k} \dots w_{1}) \in A, w_{j} \in \Sigma } \end{align}
concatenation
\begin{equation} A \cdot B = \{vw | v \in A, w \in B\} \end{equation}
clean star
\begin{equation} A^{*} = \qty {s_1 \cdot \dots \cdot s_{k} | k \geq 0, s_{i} \in A} \end{equation}
note that, since \(k\) can \(=0\), \(A^{*}\) always includes the empty string as that’s nothing concatenated
operations on regular languages are regular
if \(A, B\) are regular languages, their union, intersection, complement, reverse, concatenation, star are all regular languages.
proof
union
we have:
\begin{align} A \cup B = \qty {w | w \in A\ OR\ w \in B } \end{align}
we desire that \(A \cup B\) is regular. Let’s create two DFA for which \(A\) and \(B\) are valid languages; that is, \(A \in L(M_1)\), \(B \in L(M_2)\). we want to create some \(M\) that would recognize \(A \cup B\).
Idea: “run \(M_1\) and \(M_2\) ‘in parallel’”. For \(M = (Q, \Sigma, \delta, q_0, F)\), let’s define…
\begin{equation} Q = Q_1 \times Q_2 \end{equation}
whereby each state is a tuple of states from \(M_1\) and \(M_2\).
\begin{equation} q_0 = \qty(q_0^{(1)}, q_0^{(2)}) \end{equation}
\begin{equation} F = \qty {(q_1, q_2) | q_1 \in F_2\ OR\ q_2 \in F_2} \end{equation}
for a new symbol in the alphabet \(\sigma\), we have:
\begin{equation} \delta((q_1,q_2), \sigma) = (\delta_{1}(q_1, \sigma), \delta_{2}(q_2, \sigma)) \end{equation}
intersection
we have:
\begin{equation} \begin{align} A \cap B = \qty {w | w \in A\ AND\ w \in B } \end{align} \end{equation}
we desire \(A \cap B\) is regular.
Its the same proof as the union theorem above, we just need to change our accepting states
\begin{equation} F = \qty {(q_1, q_2) | q_1 \in F_2\ AND\ q_2 \in F_2} \end{equation}
complement
we have:
\begin{align} \neg A = \qty {w \in \Sigma^{*} | w \not \in A} \end{align}
we want to build an automata for which it will accept everything that’s not in \(A\). We can do this by just flip accept and reject states: \(F’ = \{q | q \not \in F\}\).
reverse
this one will give us “a little bit of trouble”
\begin{align} A^{R} = \qty {(w_{1} \dots w_{k}) | (w_{k} \dots w_{1}) \in A, w_{j} \in \Sigma } \end{align}
we desire \(A^{R}\) is also regular.
Insight: we need to build a DFA that reads its strings from right to left.
If \(M\) accepts some word \(w\), then \(w\) describes a directed path from start to accept state. How about we build a reverse path from the accept state to the start state? Problem: doing this may not necessarily be a DFA! It may have many start states which have different paths; also, some states may have more than one outgoing edge for a particular character, or none at all
To fix this, we say our new machine accepts a string if there exists some path that reaches some accept state from some start state. This is a Nondeterministic Finite Automata!!
Proof (by construction):
- reverse the arrows of your DFA that you want to reverse
- flip the DFA’s start and accept states
- you now have an NFA
- use subset construction to expand this NFA to a DFA
concatenation
\begin{equation} A \cdot B = \{vw | v \in A, w \in B\} \end{equation}
Proof idea:
treat your DFA as a NFA, then glue (“add epsilon transitions between”) the accept states from the first part to the start staates of the second part. then, turn the accept states in the first part into regular states.
then subset construction.
clean star
\begin{equation} A^{*} = \qty {s_1 \cdot \dots \cdot s_{k} | k \geq 0, s_{i} \in A} \end{equation}
proof idea:
stick epsilon transitions between your accept states and your original start state; and—to deal with the empty set—also add an accept state as your start state, and add an epsilon transition from that to your actual start state
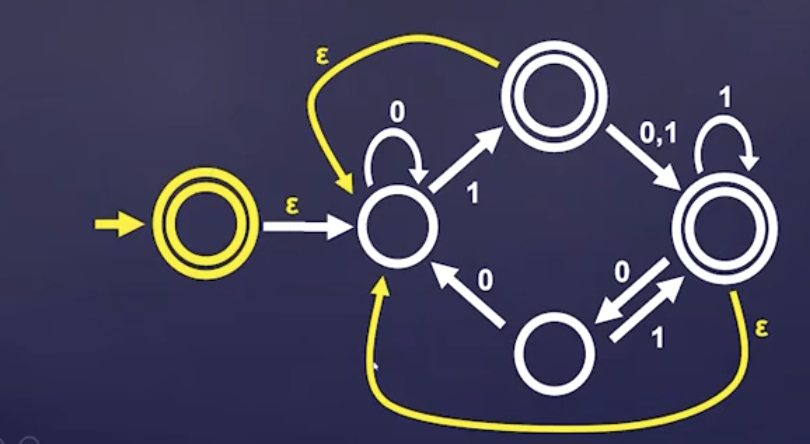
proof (construction):
- \(Q’ = Q\cup \qty {q_0}\), where \(q_0\) is our new empty string acceptor; we relabel \(q_1\) as pour original start vertex
- \(F’ = F \cup \qty {q_0}\)
and transitions:
\begin{equation} \delta’(q,a) = \begin{cases} \qty {\delta (q,a)}, q\in Q, a \neq \varepsilon \\ \qty {q_1}, q \in F, a = \varepsilon \\ \qty {q_1}, q &= q_0, a = \varepsilon \\ \emptyset, q &= q_0, a \neq \varepsilon \end{cases} \end{equation}
we are going to show this in a standard double containment.
\(L(N) \supseteq L^{*}\)
Assume you have \(w \in L^{*}\), by definition this means that \(w\) can be split into a series of \(w_1, …, w_{k}\) each of which is in \(L\).
we show that each \(w\) is accepted by induction; the base cases are \(k=0\), where its directly accepted, or \(k=1\), then since \(w_1 \in L\), we are done.
invariant is that our substring \(k\) so far is accepted.
the inductive step: to concatenate one more, since string up to \(k\) is accepted, we are at an accept state; we use the epsilon steps to get to the start of \(M\); by definiton \(w_{k+1}\) is also accepted, so we will end back at accept state, and we are done.
\(L(N) \subseteq L^{*}\)
assuming we have some string \(w\) accepted by \(N\); we desire that \(w \in L^{*}\). This means that we can break \(w\) into substrings in \(L\).
if \(w = \varepsilon\), then \(w \in L^{*}\).
induction again. IH: if \(N\) accepts \(u\) after at most \(k\) \(\varepsilon\) transitions, then \(u \in L^{*}\).
base: 0 epison transitions means you have the empty string, which is in the
induction: we divide \(w\) as \(uv\), where \(v\) is the substring after the last \(\varepsilon\) transition. we can see that \(u \in L(N)\) because episode transitions only happen in our construction at accept states—by the inductive hypothesis, we have that \(u \in L^{*}\). now, we have \(v\), which takes us from the last epsilon transition all they way to an accept state (because recall \(w\) is in \(N\)), meaning \(v \in L\) because by design we went from a start state to an accept state without taking any epsilon transitions. finally, since \(u \in L^{ *}\), concatenating another thing in \(L\) to it also gives a thing in \(L^{ *}\), so \(uv \in L^{ *}\).