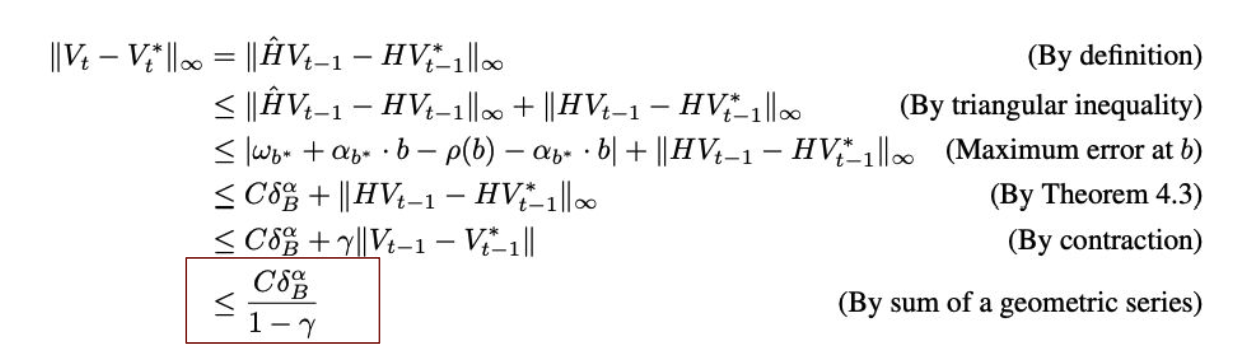POMDPs to solve Active Sensing Problem: where gathering information is the explicit goal and not a means to do something. Meaning, we can’t train them using state-only reward functions (i.e. reward is based on belief and not state).
Directly reward the reduction of uncertainty: belief-based reward framework which you can just tack onto the existing solvers.
To do this, we want to define some reward directly over the belief space which assigns rewards based on uncertainty reduction:
\begin{equation} r(b,a) = \rho(b,a) \end{equation}
\(\rho\) should be some measure of uncertainty, like entropy.
key question: how does our POMDP formulations change given this change?
Don’t worry about the Value Function
result: if reward function is convex, then Bellman updates should preserve the convexity of the value function
So, we now just need to make sure that however we compute our rewards the reward function \(\rho\) has to be piecewise linear convex.
PWLC rewards
One simple PWLC rewards are alpha vectors:
\begin{equation} \rho(b,a) = \max_{\alpha in \Gamma} \qty[\sum_{ss}^{} b(s) \alpha(s)] \end{equation}
We want to use \(R\) extra alpha-vectors to compute the value at a state.
This makes our Belman updates:
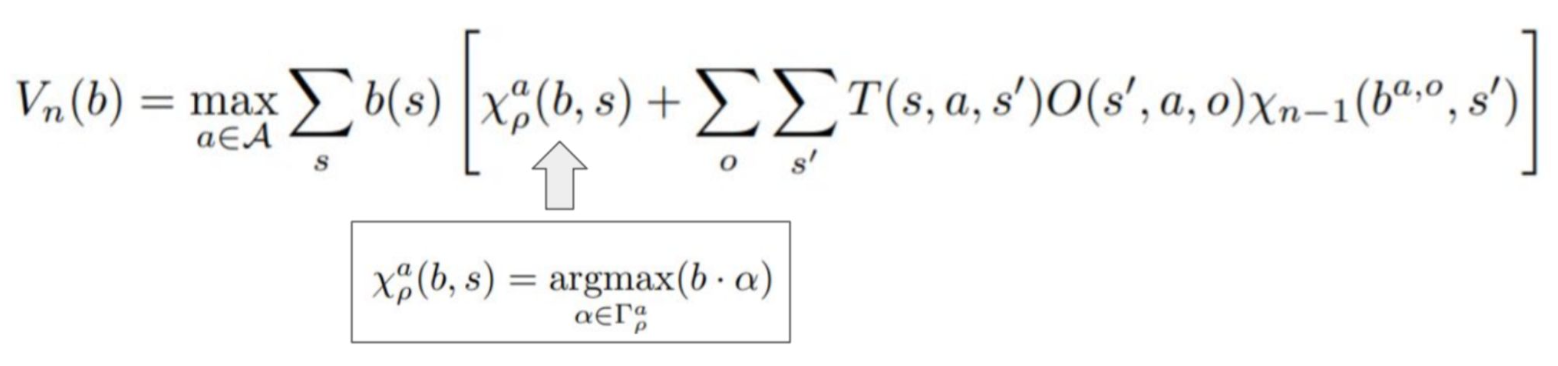
non-PWLC objectives
As long as \(\rho\) is convex and stronger-than Lipschitz continuous, we can use a modified version of the Bellman updates to force our non PWLC \(\rho\) into pretty much PWLC:
\begin{equation} \hat{\rho}(b) = \max_{b’} \qty[\rho(b’) + (b-b’) \cdot \nabla p(b’)] \end{equation}
Taylor never fails to disappoint.
Fancy math gives that the error in this would be bounded: