Building a programing language, step by step:
Lambda Calculus
\begin{equation} e \to x | \lambda x.e | e\ e \end{equation}
and you can add types
\begin{equation} e \to x | \lambda x: t.e | e\ e | i \end{equation}
\begin{equation} t \to \alpha | t \to t | \text{int} \end{equation}
Adding ADT
\begin{equation} \lambda a_1 . \lambda a_2 \dots \lambda a_{k}. \lambda f_1 . \lambda f_2 \dots \lambda f_{n} f_i a_1 a_2 \dots a_{k} \end{equation}
possible encodings
- Non-Negative Integers
- Pair
- Booleans
- Binary Trees
Constants
You can add natively….
- integers
- +, *, -, etc.
- strings
- arrays
- booleans
- …
We build these in to obtain good hardware support.
Controls
\begin{equation} \text{if}: \text{Bool} \to t \to t \to t \end{equation}
where each \(t\) is an expression.
In a call by value language, this has to be a built-in construct because otherwise each of the arms will be evaluated first before if (which is disastrous because it kind of obviate the point of the if).
\begin{equation} \frac{A \vdash e_1 : \text{Bool}, A \vdash e_2: t, A \vdash e_3:t}{A \vdash \text{if } e_1 e_2 e_3 : t} \end{equation}
and to perform type inference
\begin{equation} \frac{A \vdash e_1: \text{Bool}, A \vdash e_2 :t_1, A \vdash e_3: t_2, t_1 = t_2}{A \vdash \text{if } e_1 e_2 e_3 : t_1} \end{equation}
Recursion
Let us define a recursive function definition:
\begin{equation} \text{letrec } f = \lambda x . e_1\ \text{in}\ e_2 \end{equation}
this is different from normal let because we want recursive functions, meaning we want \(e_1\) to be able to use/call \(f\).
We define this via:
\begin{equation} \qty(\lambda f . e_2) \qty(Y \lambda f. \lambda x . e_1) \end{equation}
where, recall y-combinator:
\begin{equation} Y = \lambda f. \qty(\lambda x. f (x x)) (\lambda x. f (x x)) \end{equation}
Type checking for recursion:
\begin{equation} \frac{\begin{align} &A, f : t_1 \to t_2 \vdash \lambda x. e_1: t_1 \to t_2 \\ &A, f : t_1 \to t_2 \vdash e_2 : t \end{align}}{A \vdash \text{letrec } f = \lambda x.e_1 \text{ in } e_2: t} \end{equation}
notice this is different from a normal let because the first term also has available the type of \(f\), making this a recursive procedure.
Notice the type of \(f\) is underspecified; to make this happen, we use type inference:
\begin{equation} \frac{\begin{align} &A, f : \alpha \to \beta \vdash \lambda x. e_1: t_1 \to t_2 \\ &A, f : \alpha \to \beta \vdash e_2 : t \\ &\alpha = t_1\ \beta = t_2 \end{align}}{A \vdash \text{letrec } f = \lambda x.e_1 \text{ in } e_2: t} \end{equation}
(you could quantify the bottom expressions; trying to make the top of the let—i.e. the recursion—polymorphic makes the result undecidable).
Parametric Polymorphism
\begin{equation} e \to x | \lambda x . e | e\ e | \text{let} f = \lambda x.e \text{ in } e | i \end{equation}
\begin{equation} t \to \alpha | t \to t | \text{int} \end{equation}
\begin{equation} o \to \forall a . o | t \end{equation}
to avoid code duplication (because functions could now be polymorphic)
Subtyping
For instance, suppose you have an if statement that allowed different types
\begin{equation} \frac{\begin{align} &A \vdash e_1 : \text{Bool} \\ &A \vdash e_2: t_1 \\ &t_3 = \text{lub}\qty(t_1, t_2) \end{align}}{A \vdash e_1 ? e_2 : e_3 : t_3} \end{equation}
where \(lub\) is the least-upper-bound: the one, smallest type which is the supertype of both \(t_1\) and \(t_2\)
Notice this only makes sense where your type hierarchy is a tree (meaning single inheritance).
Overloading
\begin{align} &+: \text{int} \to \text{int} \to \text{int} \\ & +: \text{float}\to \text{float}\to \text{float}\\ & +: \dots \end{align}
overloading with subtyping is, therefore, complicated.
Functional Languages
At this point we have succeeded in building functional languages—
- all: lambdas + primitives + ADTs
- with polymorphism: ML, OCaml, Haskell
Monads
A consequence of this is to be able to pump a generalized “state” through computation. Many language features can be monads—state, continuations, exceptions, threads, etc.
Haskell’s key idea: make your own monads, and scope them! Notice that since they carry state, they are really single-threaded in the sense that they are best done with coroutines.
Objects
Objects are something fundamentally different. Typed OOP languages can’t really be translate into typed functional languages because unrestricted method overrides is impossible to type (if there is runtime function swapping with new types).
OOP vs. Functional Language
Functional language
- adding a new function is a local change
- adding a new kind of data (i.e. a new constructor), it requires updating every function that takes that type
OOP language
- adding a new data is a local change
- adding a new function (method) requires updating many classes with a definition of that method (perhaps mostly automatic through inheritance)
Extending OOP to Functional Languages
Haskell typeclasses! In some sense this is closer to Java “interfaces” than objects—interfaces has a performance hit compared to inheritance, but do support systems better.
some typeclasses
“supporting object equality”
(==) :: Eq a => a -> a -> bool
“supporting object ordering”
(<) :: Ord a => a -> a -> bool
code that require certain functionality can require a value of the appropriate type class without details to implementation (i.e. we only guarantee specific methods existing but not how they are implemented).
Extending Functional Languages to OOP
- C++ has lambdas since C++14
- Java had lambdas since Java8
- Polymorphic types: C++ has templates(ish, because C++ actually instantiates templates after type checking), Java ha generics
Invariant Inference
This is a bonus topic that just isn’t caused anywhere.
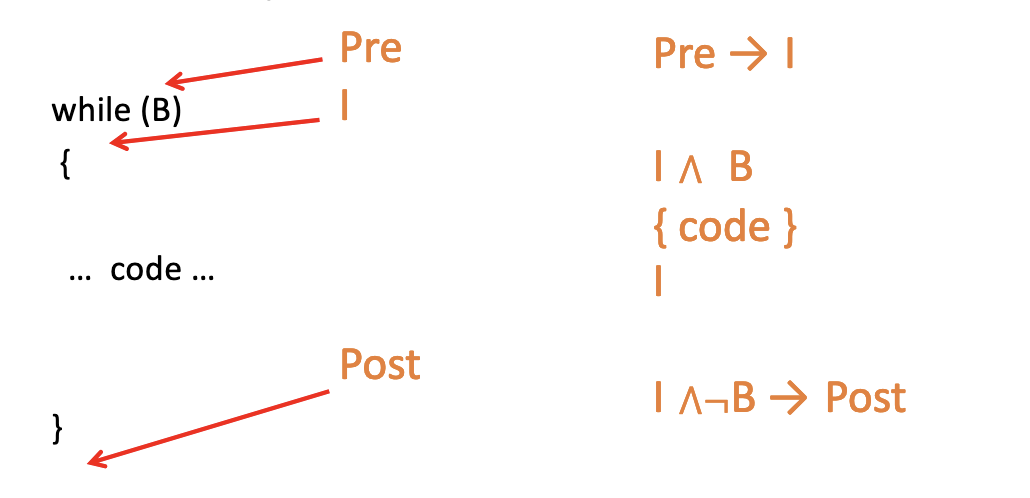
Suppose \(I\) is an inductive loop invariant. Notice in the {code} segment we don’t assume that our invariant is true; the invariant could disappear and get reestablished.
We also only have to show this once through the loop, for all desired preconditions.
Inferring what invariants are there is still an active research topic.