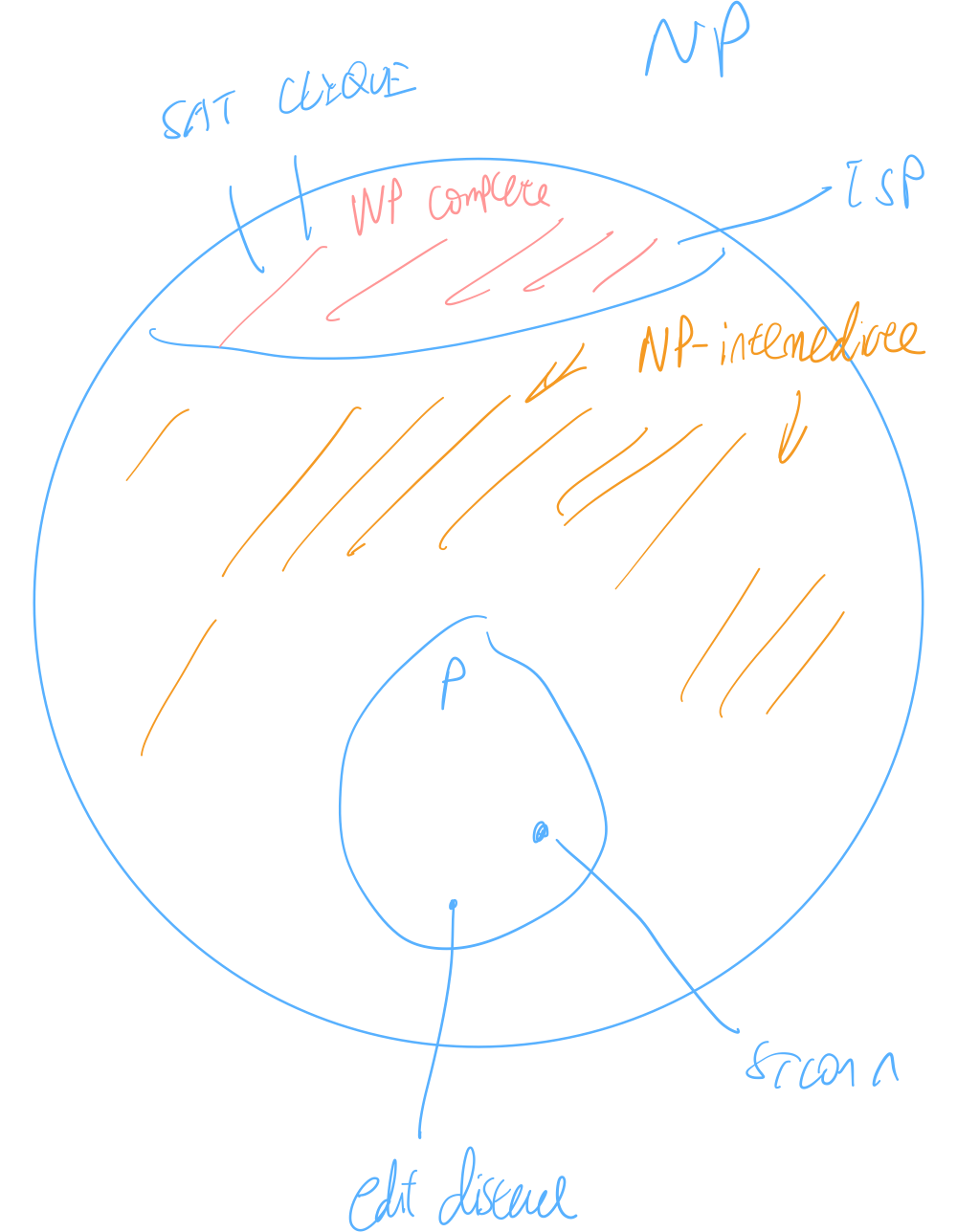
NP-Intermediate
If \(P = NP\), then no distinction between \(P\) and \(NP\), but…
If \(\text{P} \neq \text{NP}\), then exists “NP-intermediate” problem such that \(L \in \text{NP}\) such that \(L \not \in P\) and \(L\) is not NP-complete.
But today, we will prove a weaker’s version.
Ladner’s Theorem
Weaker’s Ladner’s theorem:
Assuming \(\text{SAT}\) requires \(2^{\Omega\qty(n)}\), then there are NP-intermediate languages.
PadSAT
Consider:
\begin{equation} \text{PadSAT}_{m} = \qty {\langle \varphi, 1^{m} \rangle : \varphi \in \text{SAT}} \end{equation}
This is easier than SAT since you have a bigger \(n\) artificially, and you can throw away the \(m\).
Proof idea
Choose \(m\) appropriately so that PadSAT falls in the sweet spot between \(P\) and \(NP\) complete. In particular, we choose:
\begin{equation} \text{PadSAT} = \qty { \langle \varphi, 1^{2^{\sqrt{|\varphi|}}} \rangle, \phi \in \text{SAT}} \end{equation}
Meaning, \(N = n+2^{\sqrt{n}}}=2^{\theta\qty(\sqrt{n})}\).
We show three things:
- PadSAT is in NP (witness is just the satisfying assignment)
- PadSAT not in P
- PadSAT is not NP-Complete
PadSAT not in P
PadSAT is not in P
Assume for contradiction PadSAT is in P, meaning \(\exists\) algorithm in polytime that decides PadSAT in poly(N) time; there is an \(2^{\theta\qty(\sqrt{n})}\) time algorithm for SAT.
- pad the input to length using \(2^{\theta\qty(\sqrt{n})}\) time
- solve using the oracle, which takes at most \(2^{\theta\qty(\sqrt{n})}\) time
note that this contradicts our assumption that SAT is in \(2^{\Omega\qty(n)}\).
PadSAT is not NP-Complete
PadSAT is not NP complete
Suppose for the sake of contradiction that PadSAT is NP-complete. We will see that \(\text{SAT} \leq_{P} \text{PadSAT}\), which contradictions the assumption.
Consider: \(\Phi \stackrel{?}{\in} \text{SAT}\) with \(N = |\Phi|\) where, after a Poly(N) reduction, we have \(\langle \varphi, 1^{2^{\sqrt{|\phi|}}} \rangle\) where \(\Phi \in \text{SAT} \Leftrightarrow \varphi \in \text{SAT}\) by the assumption.
Now, consider what \(|\varphi| = n\) is in terms of \(N\):
- \(n + 2^{\sqrt{n}} = \text{poly}\qty(N)\)
- IFF \(2^{\theta \qty(\sqrt{n})} = \text{poly} \qty(N)\)
- IFF \(\theta \qty(\sqrt{N}) = \theta \qty(\log N)\)
- IFF \(n = \theta \qty(\log^{2} N)\)
this is compression! Meaning, we can run an extraction procedure