Say we want to find the number which is the additive inverse (“negative”) of a number.
We can just flip each of the digit, and then add 1:
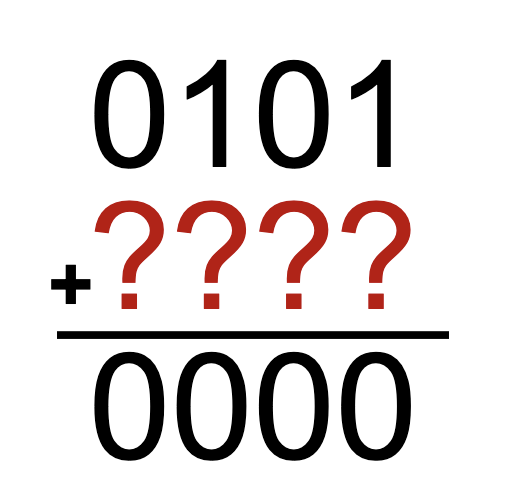
- take \(0101\), invert it to get \(1010\)
- adding these two numbers will give you \(1111\). If we just added one more \(0001\), it will flip over to be \(0000\).
- Therefore, \(1010+0001 = 1011\) is the additive inverse of \(0101\).
The left most bit being one: still a mark of whether or not something is negative. It just works backwards:
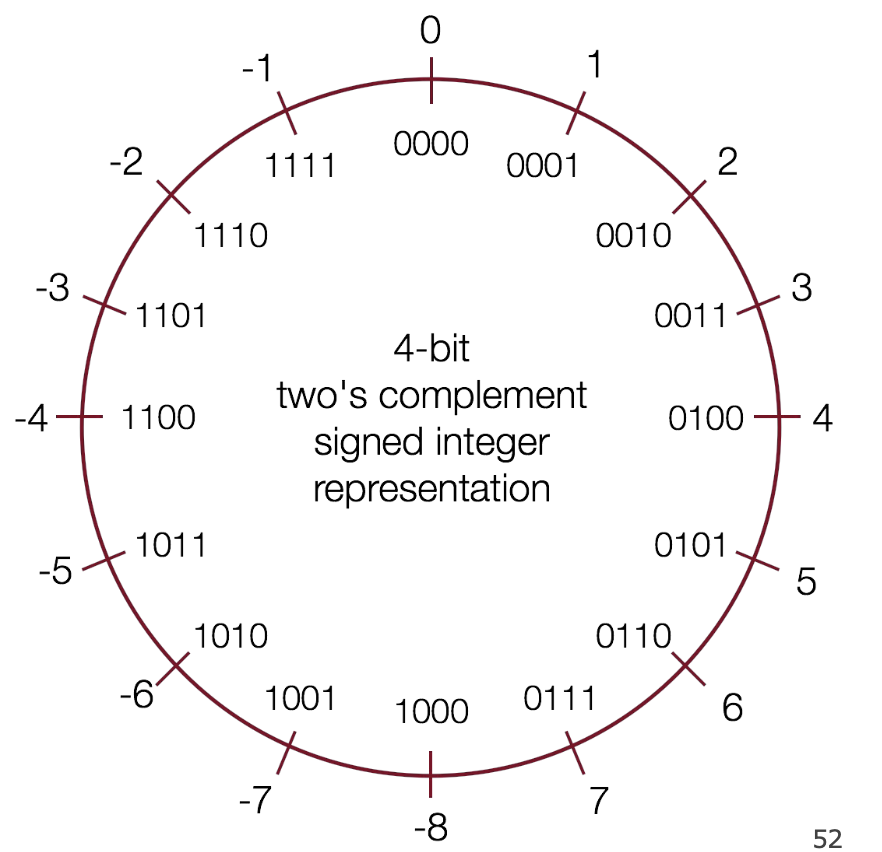
pros and cons of twos complement
- con: more difficult to represent and difficult to convert
- pro: only 1 representation for 0
- pro: the most significant bit still indicates the sign of a number
- pro: addition works for any combination of positive/negative
tricks
- all zeros: its always 0
- zero plus all ones (011111…111): it always is the largest signed value and some middle value for unsigned
- all ones: its always -1 (11111 => 00000 +1 => 1) for signed
- one plus all zeros
mnemonic for remembering where overflows happened
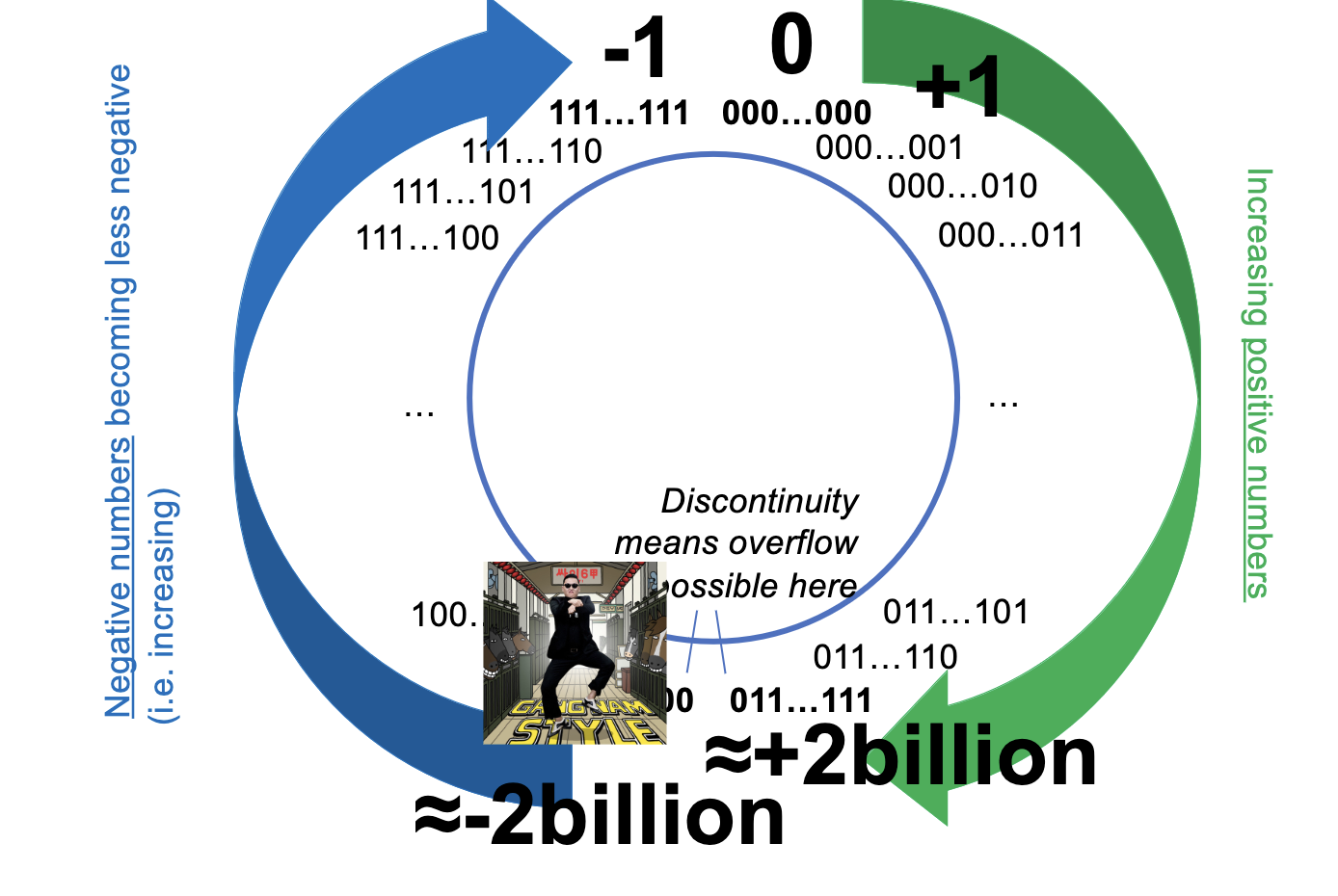
Unsigned
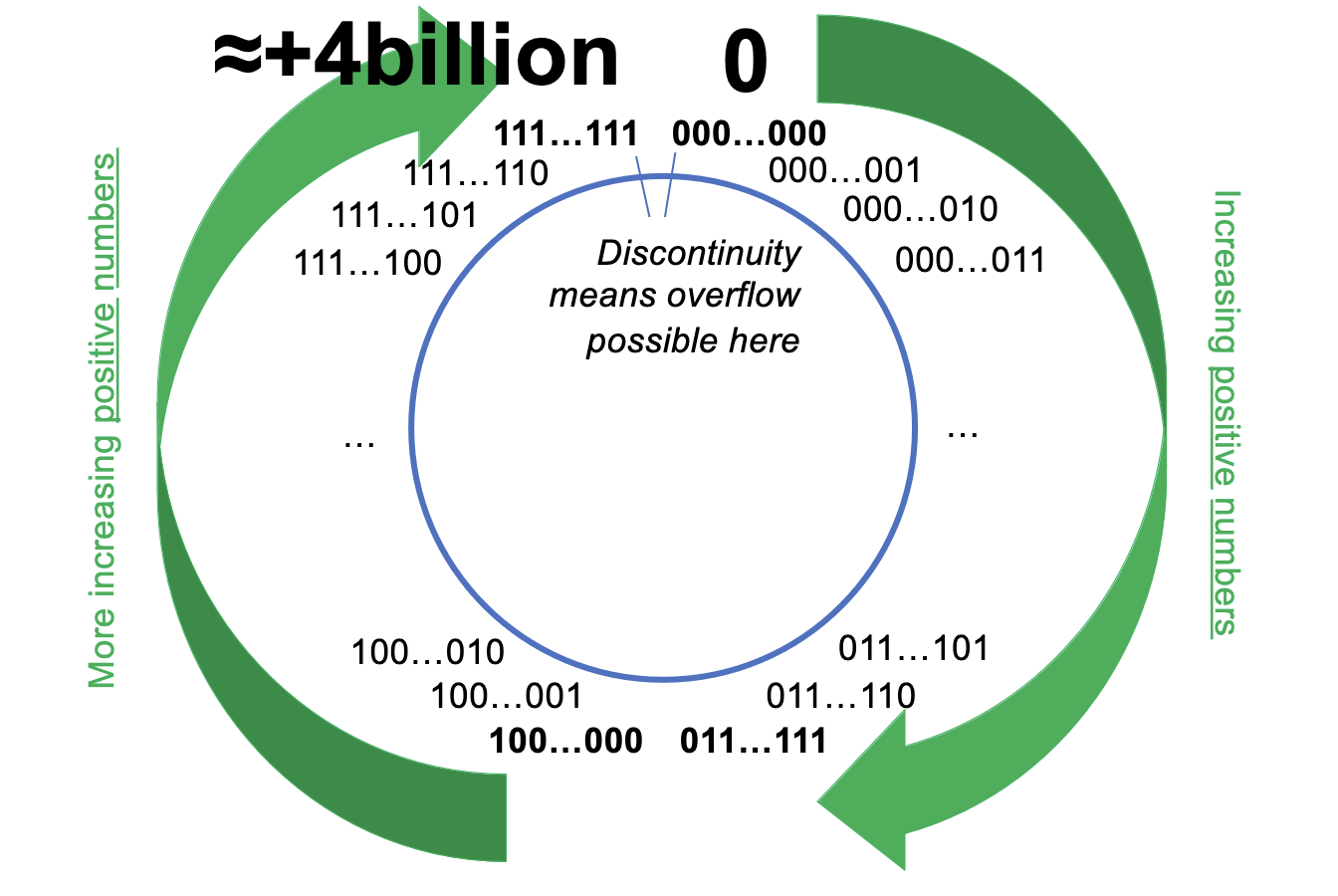
Signed