bootstrap
Last edited: August 8, 2025bootstrap allows you to know distribution statistics, calculate p-value, etc, with NO statistical testing like t test, etc.
Big idea: treat your sample space as your population, and sample from it to obtain an estimate of the properties of the sample distribution.
\begin{equation} D \approx \hat{D} \end{equation}
so, to calculate the distribution of any given statistic via a sample:
- estimate the PMF using sample
my_statistic_dist= [] (like sample mean, sample variance, etc.)- for i in (N >> 10000)
- take a
subsampleof len(sample) samples from PMFu my_statistic_dist.append(my_statistic=(=subsample)) (recall it has to be a sampling statistic (like N-1 for sample variance)
- take a
- how you have a distribution of
my_statistic
We know that taking mean and var re drawn as a statistic of the same random variable, \(N\) times. So, central limit theorem holds. Therefore, these are normal and you can deal with them.
Boston Naming Test
Last edited: August 8, 2025BNT is a discourse task where subjects are shown 60 pictures decreasing frequency and asked to recall the word.
Bouton 2018
Last edited: August 8, 2025One-Liner
Uses the single-user avoidance POMDP formulation presented in (Bouton, Cosgun, and Kochenderfer 2017) to extend to multiple road users
Novelty
Uses Single-User Model of Road Navigation to extend general POMDP formulation into multi-pedestrian/multi road user casesroad user cases
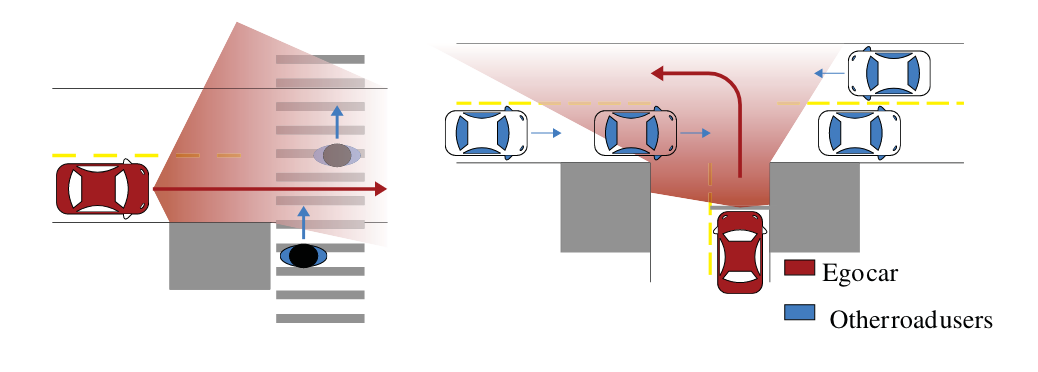
Previous Work
Imagine worst-case scenario always: set upper bound and always imagine it; could cause gridlock if situation never resolves.
Notable Methods
Uses QMDP and SARSOP to perform optimization
Single-User Model of Road Navigation
Branch and Bound
Last edited: August 8, 2025Big idea: keep branching/selecting until a tally hits an upper/lower bound
Ingredients:
- \(Ulo(s)\): lower bound function of value function
- \(Qhi(s,a)\): upper bound function of action-value function
- \(\mathcal{P}\) problem (states, transitions, etc.)
- \(d\) depth (how many next states to look into)—more is more accurate but slower
Its Forward Search, but with bounds instead of exponentially looking into every possible next state, we only check the actions in the order of their bounded value. We start with the actions with the highest bound (most possible value), and if its already better than the upper bound, we can be done because we know everything else will have lower value as their bounds are lower.
Braun and Clarke thematic analysis
Last edited: August 8, 2025Way of performing action research developed by Victoria Clarke and Virginia Braun in 2006
