Courses to Take for QNLP
Last edited: August 8, 2025- CS157 Introduction to Logic; Carta average 3.9, “Only take if you are actually interested in logic or this is an absolute requirement for your degree that you can’t dodge. Class structure is very tricky as your entire grade depends on how you do on 3 exams of 5 questions each.”
covariance (probability)
Last edited: August 8, 2025\begin{equation} cov(x,y) = E[(X-E[X])(Y-E[Y])] = E[XY]-E[X]E[Y] \end{equation}
(the derivation comes from FOIling the two terms and applying properties of expectation.
we want to consider: if a point goes way beyond its expectation, does the corresponding point change for another?
\begin{equation} (x-E[x])(y-E[y]) \end{equation}
if both points are varying .
Instead of using this unbounded value, we sometimes use a normalized value named correlation:
\begin{equation} \rho(X,Y) = \frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}} \end{equation}
we can express this in terms of a covariance matrix
covariance matrix
Last edited: August 8, 2025- diagonal slots: how do the variables vary with themselves
- off-diagonal slots: how do the variables vary with each other
coveather
Last edited: August 8, 2025coveather is a novel consensus algorithm based on the proof of work mechanism.
See also minimum user base requirements for coveather and Coveather Abstract.
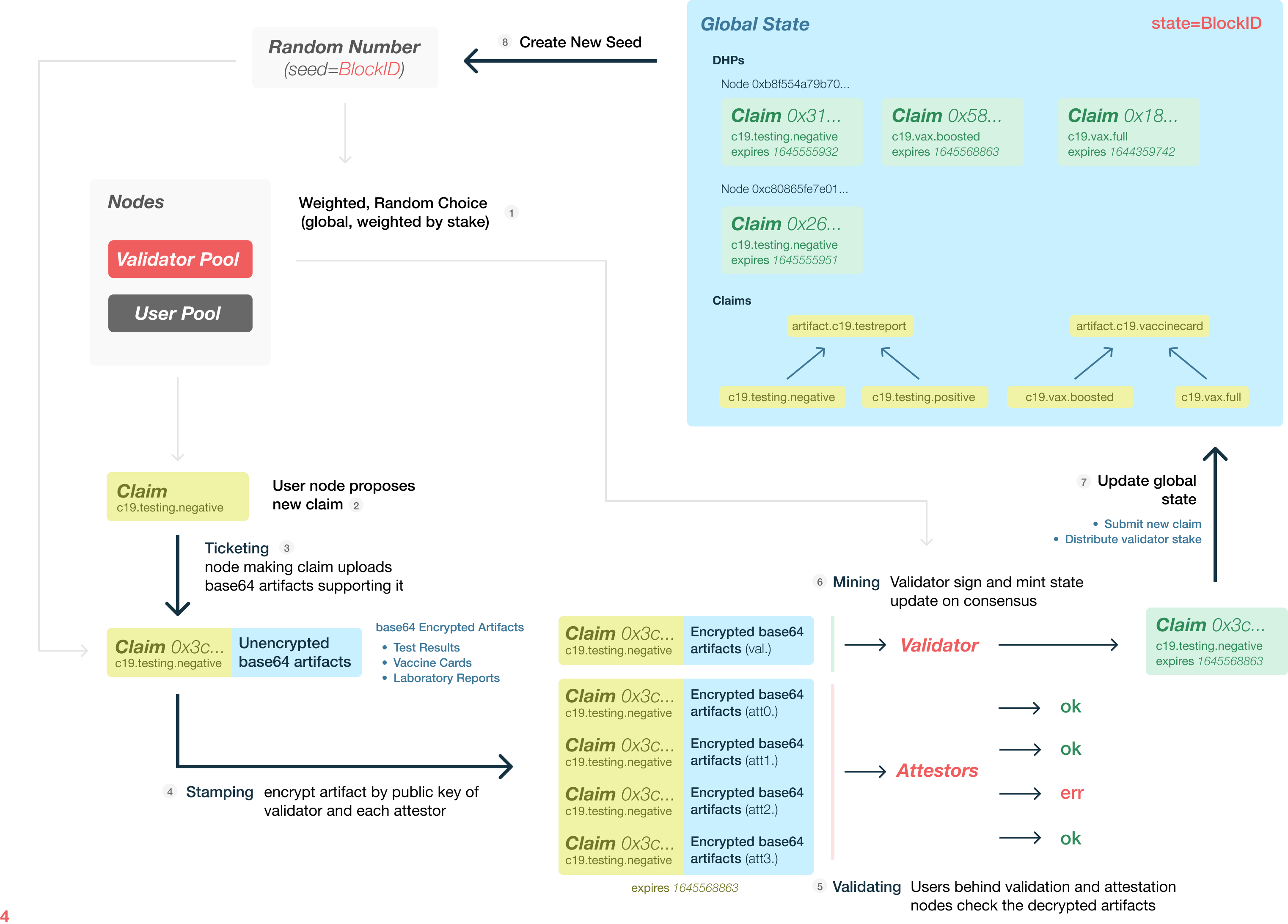
Coveather Abstract
Last edited: August 8, 2025Digital Health Passes (DHP), systems of digitally validating quarantine and vaccination status such as the New York IBM Excelsior Pass, demonstrate a lawful means to approach some benefits offered by “true elimination” treatment strategies-which focus on the complete elimination of cases instead of investing more in controlling the progression of the disease-of COVID-19. Current implementations of DHPs require region-based control and central storage of Protected Health Information (PHI)-creating a challenge to widespread use across different jurisdictions with incompatible data management systems and a lack of standardized patient privacy controls. In this work, a mechanism for decentralized PHI storage and validation is proposed through a novel two-stage handshaking mechanism update to blockchain proof-of-stake consensus. The proposed mechanism, when used to support a DHP, allows individuals to validate their quarantine and testing universally with any jurisdiction while allowing their right of independent movement and the protection of their PHI. Implementational details on the protocol are given, and the protocol is shown to withstand a 1% disturbance attack at only 923 participants via a Monte-Carlo simulation: further validating its stability.
