What random variable should I use?

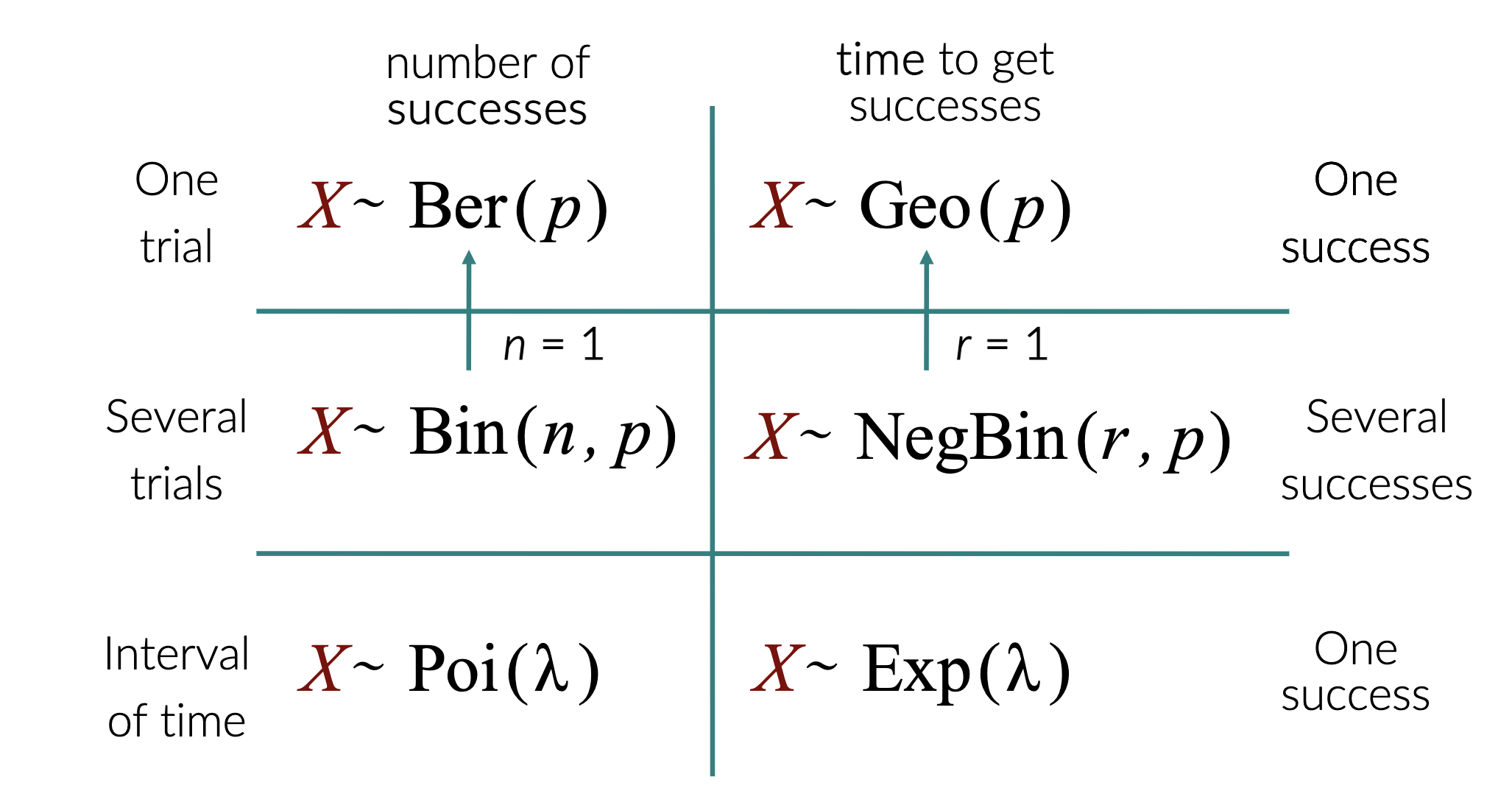
Unit 1

core probability, axiom of probability, counting, combination, permutation, DeMorgan’s Law.

• SU-CS109 SEP272023
• SU-CS109 SEP292023
• SU-CS109 OCT022023
• SU-CS109 OCT042023
• SU-CS109 OCT062023
• SU-CS109 OCT112023

Unit 2

random variables

• SU-CS109 OCT092023
• SU-CS109 OCT132023
• SU-CS109 OCT162023
• SU-CS109 OCT182023

Unit 3

inference, General Inference

• SU-CS109 OCT202023
• SU-CS109 OCT232023
• SU-CS109 OCT252023
• SU-CS109 OCT272023

Unit 4

Beta Distribution, central limit theorem, bootstrapping

• SU-CS109 NOV012023
• SU-CS109 NOV032023
• SU-CS109 NOV102023

Unit 5

Apredezahe de machinas: Naive Bayes, logistic regression, deep learning

• SU-CS109 NOV132023
• SU-CS109 NOV292023
• SU-CS109 DEC012023
• SU-CS109 DEC042023

Notes

• SU-CS109 Midterm
• SU-CS109 Midterm Sheet

Finite Automata

Deterministic Finite Automata, computability (in particular regular languages) and Non-deterministic Finite Automata (i.e. verified guessing)

optimization and Learning DFA

we were then able to characterize hardness with Streaming Algorithm and Communication Complexity

Computability Theory

turing machines, and Oracle Turing Machine, and things that are decidable vs. recognizable

through mapping reductions, we are then able to make decidability and recognizablility claims for many languages

we learned about the hierarchy of hard problems through the notion of SUPERHALT in Oracle Turing Machines

We tied mathematics and computation together, and showed Godel’s Theorem about the Limitations of Mathematics

current is defined as the flow of positive charge. Specifically:

\begin{equation} I = \frac{\Delta Q}{\Delta t} \end{equation}

resistance of a wire

(if ever you come across needing to calculate the resistance of the wire from scratch)

\begin{equation} R = \rho \frac{L}{A} \end{equation}

where, \(\rho\) is the material resistivity, \(L\) the length, and \(A\) the cross-sectional area.

you rarely need to do this!