Suppose you have two non mutually exclusive sets \(E\) or \(F\).

DeMorgan’s Law:

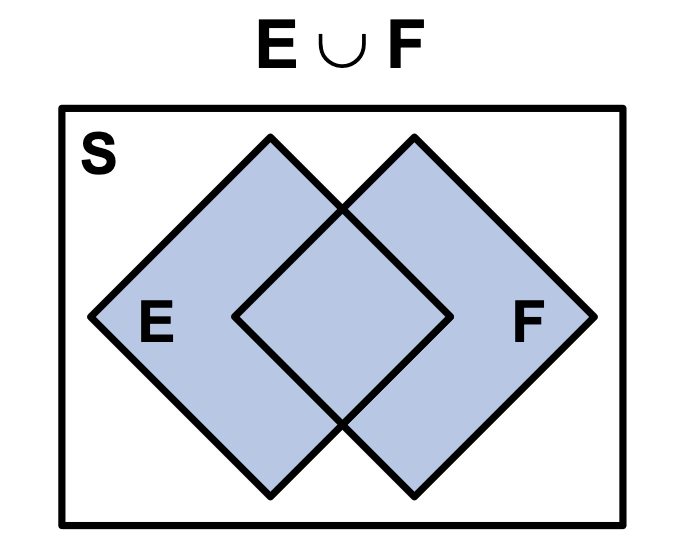
\begin{equation} (E\ and\ F)^{C} = (E^{C}\ or\ F^{C}) \end{equation}

\begin{equation} (E\ or\ F)^{C} = (E^{C}\ and\ F^{C}) \end{equation}

Derivat

a

We will take \(G(P(t),t)\) to figure the price of an option, with \(t\) being time, strike price \(X\) (not introduced yet), and expiration date \(T > t\) on a stock with price \(P(t)\) at time \(t\).

This representation does something really important: it expresses \(G\) as a function of only the current stock price \(P(t)\).