Computational Biology is a the study of biology using computation.

Rather that starting from the properties, start with the end states or what properties it has; instead, we define the initial values based on the edges.

Constructor theory: https://en.wikipedia.org/wiki/Constructor_theory?

• the relationship between temperature and occurance of a uniform gas is actually right-skewed; the mean temperature in a uniform closed system will be higher than the median temperature
• molecules are not static: at best, molecules are static when frozen in place; yet, generally it is not in their nature to stay solidly in place; they just shuffle around but maintain the molecular sturucture

If the energy level is higher, it will ignore various troughs

Time Complexity

A Computational Task:

Decision problems

1. a decision problem: \(\Sigma^{*} \to \qty {\text{no}, \text{yes}}\)
2. we often associate the “yes” instances of this decision problem as a \(L \subseteq \Sigma^{*}\) language

“Given boolean formula \(\varphi\), accept IFF \(\varphi\) is SAT”

Function problems

Give me a particular case of:

\begin{equation} f(w) : \Sigma^{*} \to \Sigma^{*} \end{equation}

note that there is a unique answer.

“Give a formula \(\varphi\), output lex first satisfying assignments/number of satisfying assignments”

bit

A computer is built out of binary gates:

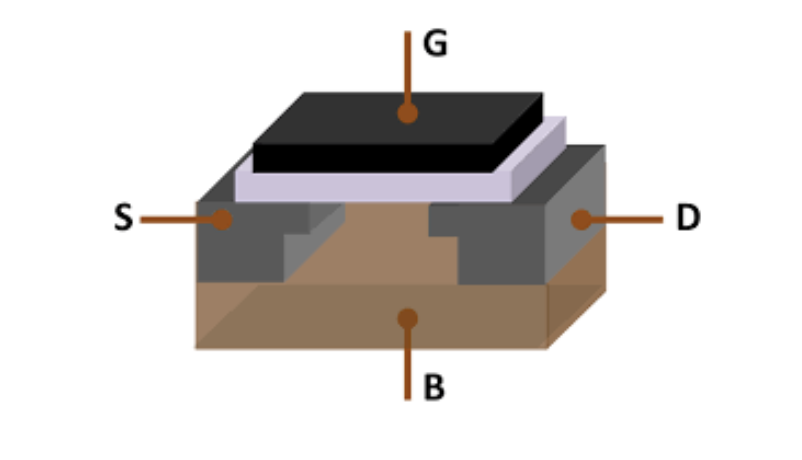
So, having voltage into \(B\) allows current to pass through between \(S\) and \(D\), it could be on/off.

byte

Accumulation of \(8\) bits

Computer memory is a large array of bytes. It is only BYTE ADDRESSABLE: you can’t address a bit in isolation.

bases

Generate, each base uses digits \(0\) to \(base-1\).

We prefix 0x to represent hexadecimal, and 0b to represent binary.