We have a system of differential equations:

\begin{equation} \begin{cases} \dv{I}{t} = -0.73 U(t) + 0.0438 + 0.4 \dv{M}{t} \\ \dv{U}{t} = 0.4I-0.012 \\ \dv{G}{t} = \dv{M}{t} - I(t) \end{cases} \end{equation}

where, \(M\) is a sinusoidal function which we can control.

We hope for this system to be as stable as possible.

First, let’s try to get a general solution of the system. The linearized(ish) solution takes the shape of:

\begin{equation} \dv t \mqty(I \\ U \\ G) = \mqty(0 & -x_1 & 0 \\ x_4 & 0 & 0 \\ -1 & 0 & 0 ) \mqty(I \\ U \\ G)+ \dv{M}{t}\mqty(x_3 \\ 0 \\ 1) + \mqty(x_2 \\ x_5 \\ 0) \end{equation}

Why do we have a market?

Basically: it allows society to make decisions about the value of things—with the wisdom of the crowd. The stock market is how we (as people) decide what to make and how to make it.

Misc. Questions About the Market

Misc. Financial Market Questions

Knowledge

• price
• Random Walk Hypothesis
• Brownian Motion
• Arbitrage Pricing
• Derivative Pricing
• options
• CAPM
• Stochastic Discount Factor
• GARCH
• ETF
• accounting price
• stock indicies
• VWAP
• short selling
• darkpool
• fundamental investing
  • Second-Level Thinking
• stock market survey
• OTC markets
• NBBO
• LiquidNet

We define:

\begin{equation} \mathbb{F}^{\infty} = \{(x_1, x_2, \dots): x_{j} \in \mathbb{F}, \forall j=1,2,\dots\} \end{equation}

closure of addition

We define addition:

\begin{equation} (x_1,x_2,\dots)+(y_1,y_2, \dots) = (x_1+y_1,x_2+y_2, \dots ) \end{equation}

Evidently, the output is also of infinite length, and as addition in \(\mathbb{F}\) is closed, then also closed.

closure of scalar multiplication

We define scalar multiplication:

\begin{equation} \lambda (x_1,x_2, \dots) = (\lambda x_1, \lambda x_2, \dots ) \end{equation}

ditto. as above

commutativity

extensible from commutativity of \(\mathbb{F}\)

The Finite Difference Method is a method of solving partial Differential Equations. It follows two steps:

1. Develop discrete difference equations for the desired expression
2. Algebraically solve these equations to yield stepped solutions

https://www.youtube.com/watch?v=ZSNl5crAvsw

Follow Along

We will try to solve:

\begin{equation} \pdv{p(t,x)}{t} = \frac{1}{2}\pdv[2]{p(t,x)}{x} \end{equation}

To aid in notation, let us:

\begin{equation} p(t_{i}, x_{j}) := p_{i,j} \end{equation}

to represent one distinct value of our function \(p\).

Let’s begin by writing our expression above via our new notation:

A graph of states which is closed and connected.

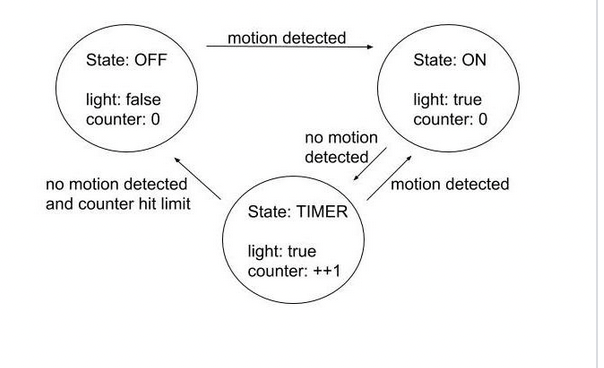
Also relating to this is a derived variable. One way to prove reaching any state is via Floyd’s Invariant Method.