Eleanor Roosevelt
Last edited: August 8, 2025Eleanor Roosevelt is the first lady of the US.
- Created minimum wage
- Wrote a weekly column named My Day, in 135 newspapers
- 2x a week broadcast
electric field
Last edited: August 8, 2025Though Coulomb’s Law allow us to calculate the force between any two individual charges, one can note that most of it is independent of the second test charge. In fact, each charge emits a field around itself of the shape:
\begin{equation} \vec{E( r)} = k \frac{q}{r^{2}} = \frac{1}{4\pi \epsilon_{0}} \frac{q}{r^{2}} \end{equation}
Or, you can think of it as moving a test charge \(q\) around the charge of interest, then calculating:
\begin{equation} \vec{E} = \frac{\vec{F_{e}}}{q} \end{equation}
electric potential energy
Last edited: August 8, 2025electric potential is analogous to gravitational potential energy, but with electrostatics!
\begin{equation} P_{E} = qV \end{equation}
where \(q\) is the change on the particle in question, and \(V\) is the voltage, the difference in electric potential between two places.
Yes, voltage is defined vis a vi electric potential: that is, it represents a differential of electric potential.
additional information
electric potential is analogous to gravitational potential
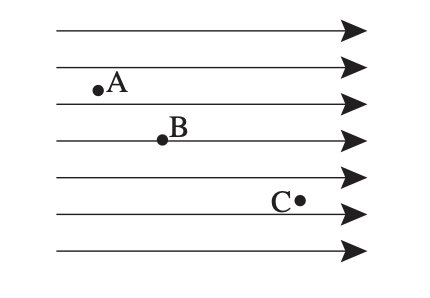
Let \(A, B, C\) be positrons, and the lines are the electric field. Which one has the highest electric potential? \(A\), because it has the most distance to travel to until it can get all the way to the right.
electron
Last edited: August 8, 2025Elie Adam
Last edited: August 8, 2025Elie Adam is a research scientist in brain dynamics and neuro-science at MIT.
Mathematical Systems
- Systemic influences with various pieces
- Hopfield Networks
Mouse Video Games
Derivatives are essentially a high pass filter
Methods of neuro imaging
- calcium channel florescence
- Electrode measurements
- Optogenetics
primary methods
- analyzing monke with neuro-imaging methods above
- creating in silico models based on those responses, in a large systems of differential equations
- play with those equations to figure possible novel responses
- try them on monke
