our ultimate goal is to create a generalized model that learns training data and extrapolate to future test data.

We don’t really care about how good we fit the training data.

key idea: fit the model on train set, and test on separate test set.

requirements

We split our training set into three parts

• training set: to fit the model
• validation set: quasi-test set
• test set: actual test (we do it only once)

additional information

root-mean-square error

this is basically least-squares error but with normalization

We want to compare features of the model to features of the data:

Visual diagnostics

1. PDF plot
2. CDF of data vs. CDF of model
3. Quantile-Quantile plot
4. Calibration Plot

Summative Metrics

1. KL Divergence
2. Expected Calibration Error
3. Maximum Calibration Error

Marginalization Ignores Covariances

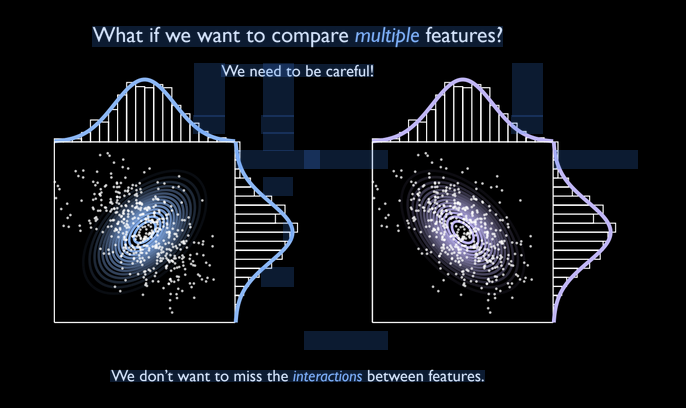
Notice on the figure on the right captures distribution much better, yet the marginal distributions don’t show this. This is because marginalizing over the datasets ignores the covariances. Hence, remember to keep dimensions and any projections hould capture covariances, etc.

An event is sub-subset of the sample space \(E \in S\). These are some subset to which you ascribe some meaning.

Have: \(m\) training data points \((\theta_{i}, \phi_{i})\) generated from the true/approximated function \(\phi_{i} = f\qty (\theta_{i})\) (which uses physical simulation/CV techniques). Training data here is *very expensive and lots of errors

Want: \(\hat{f}\qty(\theta) = f\qty(\theta)\)

Problem: as joints rotate (which is highly nonlinear), cloth verticies move in complex and non-linear ways which are difficult to handle with a standard neural network—there are highly non-linear rotations! which is not really easy to make with standard model functions using \(\hat{f}\).

Preamble

As notation differs between Alg4DM (which the presentation and notes use) and the paper, we provide a note here to standardize the notation of the PGA formulation to avoid confusion.

Recall that the non-linear program formulation of the naive PGA implementation gives:

\begin{align} \max_{\theta}\ &f(\theta) \\ \text{such that}\ &J\theta = \bold{1} \\ & \theta \geq \bold{0} \\ & h_{i}(\theta) \leq \epsilon_{i},\ \forall i \end{align}

for:

\begin{equation} f(\theta) = \beta^{\top} \bold{Z}^{-1} \bold{r}_{\theta} \end{equation}