One-Liner

UAV navigation through leveraging updrafts, handling their unpredictability with POMDPs and Receeding Horizon.

Novelty

• Developed new method for low-cost POMDP online solving
• Cool bird.

Notable Methods

two main steps

• explore: determine thermal parameters
• exploit: plan a trajectory to exploit the thermal

formulation

• \(\mathcal{S}\): \(s^{u} \in \mathbb{R}^{6}\), the joint state of the UAV (2D location wrt fixed point + air speech + heading, bank, roll, altitude), and \(s^{th} \in \mathbb{R}^{2}\),the thermal status (thermal center x and y relative to UAV)
• \(\mathcal{A}\): discretized arc trajectory segments by bank angles \(\phi_{1 \dots n}\), which executes for a fixed \(T_{A}\) seconds
• \(\mathcal{T}\): Gaussian of \(s^{u}\) over the dynamics of the UAV, and over fixed noise covariance \(Q\)
• \(\mathcal{R}\): \(h_{s’}-h_{s}\), the change in altitude….
• \(\mathcal{O}\): senor readings
• \(O(a, s’, o)\): fixed noise covariance \(R\)
• \(b_0\): product of two Gaussian of the UAV’s position and the belief about the underlying thermals
• \(update(b,a,o)\): EKF

modeling assumptions:

DOI: 10.3389/fcomp.2021.642517

One-Liner

Used WLS data to augment CTP from ADReSS Challenge and trained it on a BERT with good results.

Novelty

• Used WLS data with CTP task to augment ADReSS DementiaBank data

Notable Methods

WLS data is not labeled, so authors used Semantic Verbal Fluency tests that come with WLS to make a presumed conservative diagnoses. Therefore, control data is more interesting:

Key Figs

Table 2

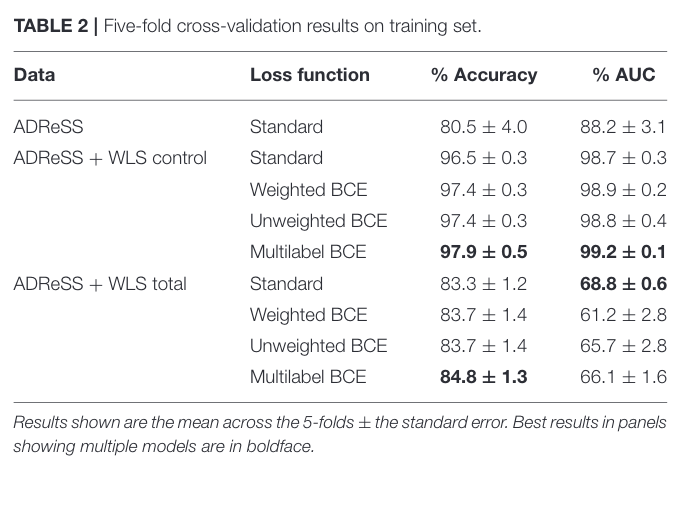
Data-aug of ADReSS Challenge data with WSL controls (no presumed AD) trained with a BERT. As expected the conservative control data results in better ferf

GUS is the a architecture of frame based Dialogue Systems; this is sometimes called a domain ontology.

General principle: try to fill as many user slots in the frame as possible that the user specifies, if the frame is filled, do action and report result.

You maybe working in multi-frame systems, then in which case some slots in one frame may help inform or fill those in another frame.

GUS uses regular expressions/grammar rules to perform all of its tasks. Generating responses are usually completely templated.

Gut bacteria are both adversly affected by 5-Fluoropyrimidine, and but they mtaybe able to inactivate synthesized Fluoropyrimidine.

PreTA in E. Coli is an example of a bacterial that can do this. See implications of PreTA deactivating Fluoropyrimidine.