if and only if
Last edited: August 8, 2025to prove that something goes both ways: given \(A\Rightarrow B\), and \(A \Leftarrow B\), \(A \Leftrightarrow B\).
If P != NP, then BPP in P
Last edited: August 8, 2025We really really want to prove:
\begin{equation} \text{BPP} \subseteq \text{P} \end{equation}
which will give \(\text{P} = \text{BPP}\).
How about we replace the truly random bits on the random tape \(r \in \qty {0,1}^{\text{poly}\qty(|x|)}\) with “pseudo-randomness” bits and prove that \(M\) can’t tell the difference.
Namely, a thing that is “pseudo-random” is easier to brute force over. So, we ideally can brute force over \(\text{poly}\qty(n)\) many outcomes instead of \(2^{\text{poly}\qty(n)}\) in the case of true randomness.
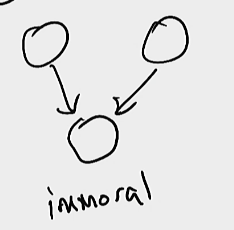
immoral v-structure
Last edited: August 8, 2025v-structure whose parents are unconnected are immoral
This is immoral:
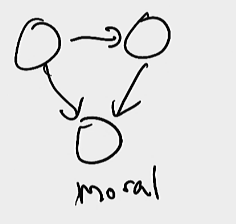
This is moral
Immunogen Design
Last edited: August 8, 2025Using a bunch of signals to create a 3d representation of the system
features
- cyro-EM
- x-ray
- tomo
- glynomics/libidomics
- genetics
studying large-scale viron behavior
Misc. Discoveries bydoing a bunch of MD
- proteins of specific virons “breath”: oning and closing an entire backbone group; this is not yet quantified in physical modeling
- when its open, the “breathing open” motion causes the virus to be vunerable
- *we don’t *
- “we are so biased by what we can see experimentally”
Immunogen Design
Last edited: August 8, 2025Using a bunch of signals to create a 3d representation of the system
features
- cyro-EM
- x-ray
- tomo
- glynomics/libidomics
- genetics
studying large-scale viron surface protein behavior using MD
“we are so biased by what we can see experimentally, so do MD”
“breathing” motion
- proteins of specific virons “breath”: oning and closing an entire backbone group; this is not yet quantified in physical modeling
- when its open, the “breathing open” motion causes the virus to be vunerable
- so some antibodies jam into the open position
“head tilting” motion
- when its tilted, there is an epitope that becomes exposed
- this is a site that’s possible for introduction of what’s needed
overall architecture
- use conventional MD
- discover regions of instability (see above for examples) for possible binding surfaces
- bam inhibition!
maybe at some point run a cyro-EM to experimentally run some
